贪心、分治
该上强度咯,这是复健计划有难度的第一题,也是我省选计划题单中的第一题。
使用 $n,m$ 表示横向道路和纵向道路的数量,使用 $q$ 表示询问次数,考虑如何回答单组询问,直接搜索的时间复杂度为 $O(2^{n+m})$ 显然无法通过。
考虑分治,每次找当前矩阵中车流量最大的道路,该道路会将矩阵分割,向出发点存在的矩阵递归即可。例如 $n=5,m=4$ 的一组询问,其中紫色格子为起点,数字为行或列被选中的轮数。然后用红色标出参与计算答案的关键点。
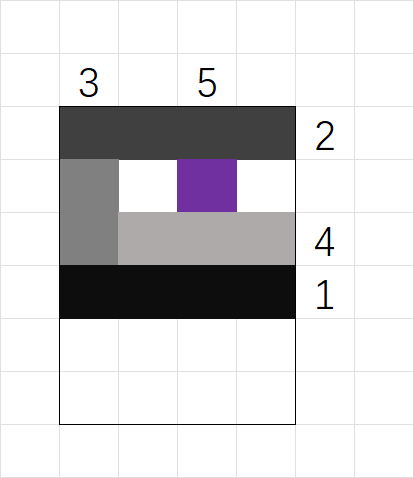

发现每条线段至多产生两个关键点,关键点答案实际上是到达这条线段后左转或右转对答案的贡献(贡献不包含在当前线段上移动的距离),无论如何这是容易计算的。
由于道路车流量两两不同,可以用两个 ST 表维护区间最值并建立值到道路编号的映射来快速找到当前矩阵中车流量最大的道路,在分治过程中按车流量从大到小计算每个线段的答案。我怀疑答案会爆 int,没有仔细分析上界而是使用了 long long 规避问题。由于我没读题导致最开始的代码只能处理从给定十字路口出发走车流量更大的道路的情况,最后的处理方法是把从 $(x,y)$ 出发向四个方向走拆成从 $(x+1,y),(x,y+1),(x-1,y),(x,y-1)$ 出发并指定方向。
由于 $n,m$ 同阶,总体时间复杂度 $O(n \log n + nq)$。
#include<bits/stdc++.h>
using namespace std;
struct SparseTable{
int n,s[18][50'005];
void resize(int x,int *w){
n=x,copy(w+1,w+n+1,s[0]+1);
for(int i=1;(1<<i)<=n;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
s[i][j]=max(s[i-1][j],s[i-1][j+(1<<(i-1))]);
}
int query(int l,int r){
int o=__lg(r-l+1);
return max(s[o][l],s[o][r-(1<<o)+1]);
}
}sn,sm;
int n,m,q,cnt,a[50'005],b[50'005],p[100'005],ex[100'005],pa[50'005][2],pb[50'005][2];
long long suma[50'005][2],sumb[50'005][2];
long long dfs(int lx,int ly,int rx,int ry,int x,int y,int t){
if(x<1||x>n||y<1||y>m) return 0ll;
if(sn.query(lx,rx)>sm.query(ly,ry)){
const int now=ex[sn.query(lx,rx)];
pa[now][0]=ly,pa[now][1]=ry;
suma[now][0]=(ly!=1)*max(now-pb[ly-1][0]+sumb[ly-1][0]+1,pb[ly-1][1]-now+sumb[ly-1][1]+1);
suma[now][1]=(ry!=m)*max(now-pb[ry+1][0]+sumb[ry+1][0]+1,pb[ry+1][1]-now+sumb[ry+1][1]+1);
if(x==now){
if(t==3) return y-ly+suma[now][0]+1;
if(t==4) return ry-y+suma[now][1]+1;
return max(y-ly+suma[now][0]+1,ry-y+suma[now][1]+1);
}
now<x ? lx=now+1:rx=now-1;
}
else{
const int now=ex[sm.query(ly,ry)];
pb[now][0]=lx,pb[now][1]=rx;
sumb[now][0]=(lx!=1)*max(now-pa[lx-1][0]+suma[lx-1][0]+1,pa[lx-1][1]-now+suma[lx-1][1]+1);
sumb[now][1]=(rx!=n)*max(now-pa[rx+1][0]+suma[rx+1][0]+1,pa[rx+1][1]-now+suma[rx+1][1]+1);
if(y==now){
if(t==1) return x-lx+sumb[now][0]+1;
if(t==2) return rx-x+sumb[now][1]+1;
return max(x-lx+sumb[now][0]+1,rx-x+sumb[now][1]+1);
}
now<y ? ly=now+1:ry=now-1;
}
return dfs(lx,ly,rx,ry,x,y,t);
}
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
for(int i=1;i<=n;i++) p[++cnt]=a[i];
for(int i=1;i<=m;i++) p[++cnt]=b[i];
sort(p+1,p+cnt+1);
for(int i=1;i<=n;i++) a[i]=lower_bound(p+1,p+cnt+1,a[i])-p;
for(int i=1;i<=m;i++) b[i]=lower_bound(p+1,p+cnt+1,b[i])-p;
for(int i=1;i<=n;i++) ex[a[i]]=i;
for(int i=1;i<=m;i++) ex[b[i]]=i;
sn.resize(n,a),sm.resize(m,b);
for(int i=1;i<=q;i++){
static int x,y;
scanf("%d%d",&x,&y);
long long ans=0ll;
for(int j=1;j<=4;j++){
static constexpr int dx[]={0,-1,1,0,0},dy[]={0,0,0,-1,1};
for(int k=1;k<=n;k++) pa[k][0]=0,pa[k][1]=0,suma[k][0]=0ll,suma[k][1]=0ll;
for(int k=1;k<=m;k++) pb[k][0]=0,pb[k][1]=0,sumb[k][0]=0ll,sumb[k][1]=0ll;
ans=max(ans,dfs(1,1,n,m,x+dx[j],y+dy[j],j));
}
printf("%lld\n",ans);
}
return 0;
}