贪心、极大子矩形类问题

首先应当明确答案只可能是一个极大子矩形，所以只需枚举极大子矩形。

极大子矩形类问题有两种解法，这道题应该使用基于障碍物数量 $n$ 的 $O(n^2)$ 做法。以下图片来自洛谷 P1578 第一篇题解。

首先把边界使用四个障碍物确定下来方便后续计算。从左到右枚举障碍物确定当前矩形左端点，每次向右找最近的一个点确定右边界，同时收缩矩形上下界。上下界重合时应当停止枚举。

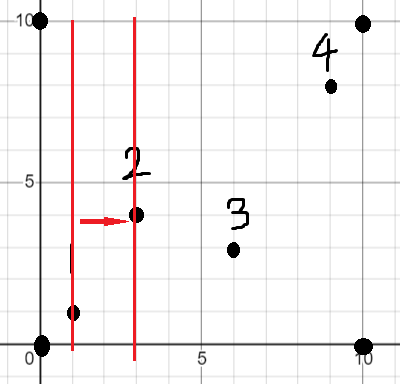
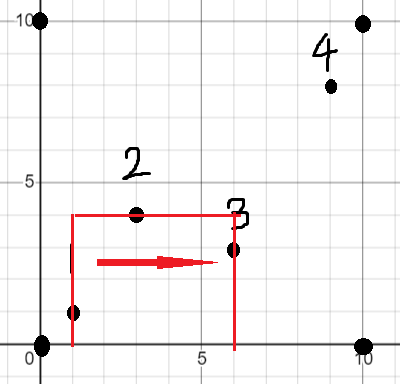
但是这样枚举会漏掉这种情况。

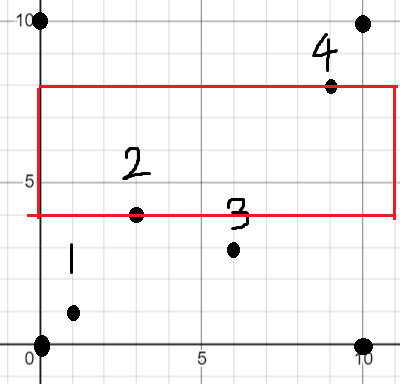
做四次坐标转换（原数据、左右翻转后的数据、坐标轴交换后的数据、坐标轴交换后左右翻转的数据）并进行四次枚举计算即可。左右翻转是因为函数中对每个点只向右枚举，缺失向左枚举的答案。枚举 $x$ 轴时 $y$ 轴是否翻转不影响答案计算，所以代码中没有复原 $x$ 轴坐标。

对四个边界进行相同的操作可以枚举所有极大子矩形。如果不把边界加入点集，就需要判断一些其他情况。注意相同 $x$ 坐标的点之间不应当相互影响。

时间复杂度 $O(n^2)$。

#include<bits/stdc++.h>
using namespace std;
struct Point{int x,y;}s[5'005];
int n,L,W,ans;
bool cmp(const Point &x,const Point &y){return x.x<y.x;}
void solution(){
    for(int i=1;i<=n;i++){
        int l=0,r=W;
        for(int j=i+1;j<=n;j++){
            if(s[i].x==s[j].x) continue;
            ans=max(ans,(s[j].x-s[i].x)*(r-l));
            if(s[i].y<=s[j].y) r=min(r,s[j].y);
            if(s[i].y>=s[j].y) l=max(l,s[j].y);
            if(l>=r) break;
        }
    }
}
int main(){
    scanf("%d%d%d",&L,&W,&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&s[i].x,&s[i].y);
    s[++n]={0,0},s[++n]={L,0},s[++n]={0,W},s[++n]={L,W};
    sort(s+1,s+n+1,cmp),solution();//原数据
    for(int i=1;i<=n;i++) s[i].x=L-s[i].x;
    sort(s+1,s+n+1,cmp),solution();//左右翻转
    swap(L,W);
    for(int i=1;i<=n;i++) swap(s[i].x,s[i].y);
    sort(s+1,s+n+1,cmp),solution();//坐标轴交换
    for(int i=1;i<=n;i++) s[i].x=L-s[i].x;
    sort(s+1,s+n+1,cmp),solution();//坐标轴交换后左右翻转
    printf("%d\n",ans);
    return 0;
}