模拟

参考图片，将奇数编号点和偶数编号点上的机器人分类讨论。

如果一个机器人向右，一个机器人向左并且它们之间没有其他机器人，它们就会撞上然后炸掉。由于机器人刚开始的位置互不相同，不可能有两个以上的机器人在同一点相撞。

配对顺序不影响计算答案，所以只要能把所有相撞的机器人配对，这道题就完成了。

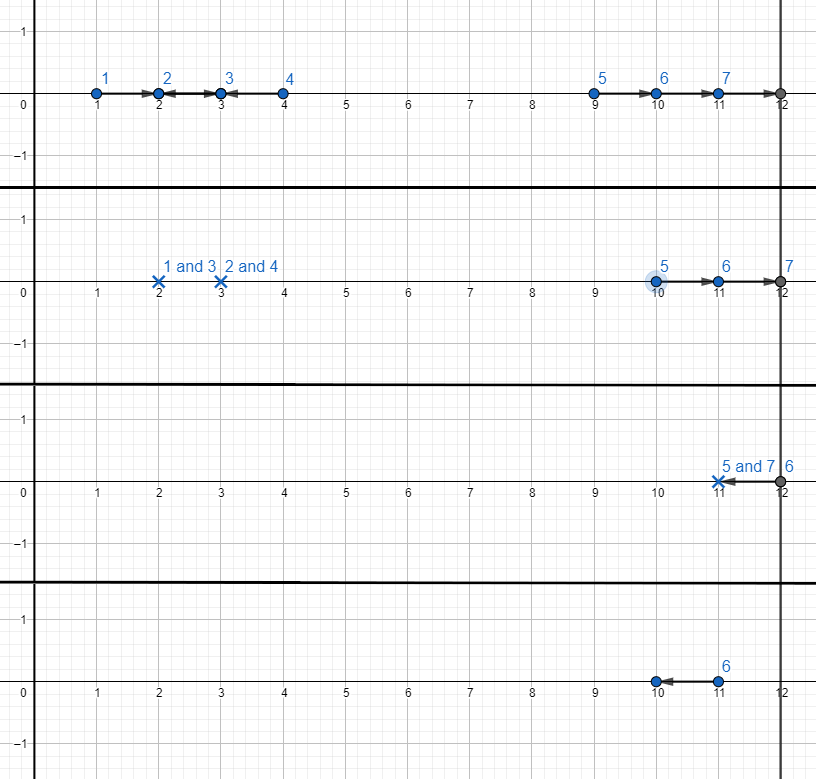
配对过程与括号匹配相同，首先枚举所有向右的机器人，如果这个机器人右边第一个机器人是向左的，就将这一对机器人配对并删除。删除后查看枚举到的这个机器人（已删除）的上一个机器人是不是向右的，如果是向右的就判断其能否配对。

枚举完成后的机器人序列形如 LLLRRRR，把边界上的 LL、RR 两两配对，如果仅剩一个机器人，那么这个机器人不会被消除，否则剩余的两个机器人必定为 LR，容易计算它们的爆炸时间。

使用 set 维护序列，时间复杂度 $O(n \log n)$。

#include<bits/stdc++.h>
using namespace std;
struct Robot{
    int x,i,r;
    Robot(int _x,int y,int z):x(_x),i(y),r(z){}
    bool operator<(const Robot &x)const{
        return this->x<x.x;
    }
};
int n,m,a[300'005],ans[300'005];
char c[300'005];
void calculate(set<Robot> s){
    auto it=s.begin(),nxt=s.end();
    while(it!=s.end()){//遍历并匹配
        if(it->r){
            nxt=next(it);
            if(nxt!=s.end()&&!nxt->r){
                int w=(nxt->x-it->x)/2;
                ans[it->i]=w,ans[nxt->i]=w;
                ++nxt,it=s.erase(it,nxt);
                if(it!=s.begin()) --it;
            }
            else ++it;
        }
        else ++it;
    }
    while(!s.empty()&&!s.begin()->r){//处理最左端
        auto it=s.begin(),nxt=next(it);
        if(nxt==s.end()||nxt->r) break;
        int w=(it->x+nxt->x)/2;
        ans[it->i]=w,ans[nxt->i]=w;
        s.erase(it),s.erase(nxt);
    }
    while(!s.empty()&&prev(s.end())->r){//处理最右端
        auto it=prev(s.end());
        if(it==s.begin()) break;
        auto nxt=prev(it);
        if(!nxt->r) break;
        int w=(m*2-nxt->x-it->x)/2;
        ans[it->i]=w,ans[nxt->i]=w;
        s.erase(it),s.erase(nxt);
    }
    if(s.empty()) return;
    if(s.size()==1) return ans[s.begin()->i]=-1,void();
    it=s.begin(),nxt=next(it);
    int w=(m*2+it->x-nxt->x)/2;
    ans[it->i]=w,ans[nxt->i]=w;
}
void solution(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>c[i];
    set<Robot> s[2];
    for(int i=1;i<=n;i++) s[a[i]&1].emplace(Robot(a[i],i,(c[i]=='R')));
    calculate(s[0]),calculate(s[1]);
    for(int i=1;i<=n;i++) cout<<ans[i]<<" \n"[i==n];
}
int T;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>T;
    while(T--) solution();
    return 0;
}