树、贪心、表达式求值
科技树缺失力(悲)。
考虑对于给定的运算序列建表达式树,举个例子 1|1&0|1&0(值为 $1$)。
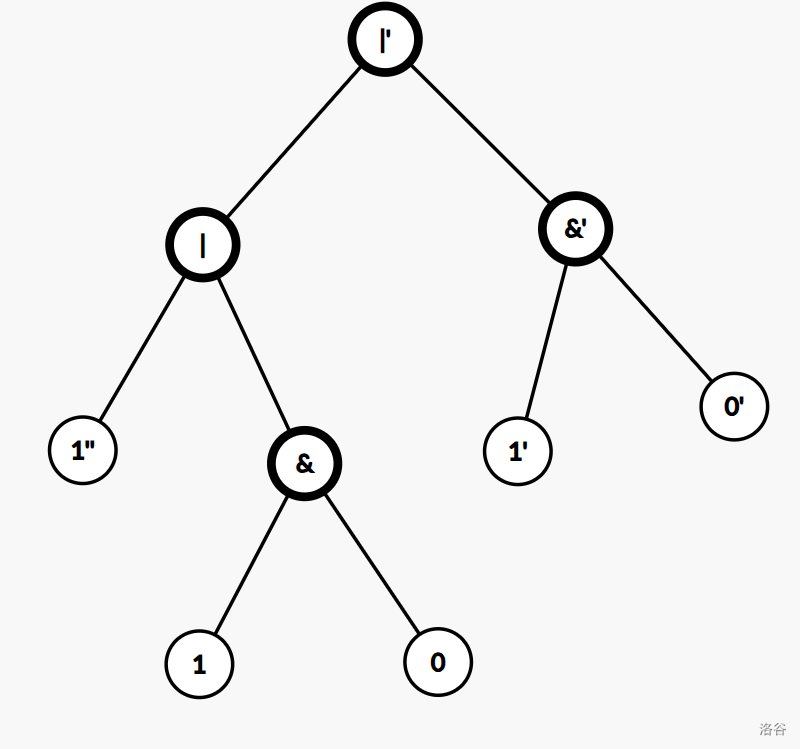
建树之后仅需一遍 dfs 即可求出两种运算的短路次数,问题转化为在 $O(n)$ 时间复杂度内根据给定中缀表达式建立表达式树。注意由于 & 运算的优先级更高,对于没有括号的式子应当先将 & 运算符提出来连边,然后再从左到右处理 | 运算符。
中缀表达式不好处理,转成后缀表达式之后再建表达式树。转换过程如下。
从左到右扫描中缀表达式,使用 $c$ 表示当前字符。
- 若 $c$ 既不是括号又不是运算符,将 $c$ 追加到后缀表达式末尾。
- 若 $c$ 为
(,将 $c$ 放入存储运算符的栈中。 - 若 $c$ 为
),将运算符栈顶不断追加到后缀表达式末尾后弹出,在栈顶为(时停止。将栈顶的(弹出。 - 若 $c$ 为运算符,将运算符栈顶不断追加到后缀表达式末尾后弹出,在栈为空、栈顶为
(或栈顶运算符优先级严格低于 $c$ 时停止。将 $c$ 放入存储运算符的栈中。
扫描结束后将运算符栈中的元素依次追加至后缀表达式末尾。
这么一来 1|1&0|1&0 就变成 110&|10&| 了。
这样看不太合理,看看 1+2*3*(5*3-2)-100 的变化,最终这个式子变成 123*53*2-*+100-,手动模拟可得实际计算顺序与中缀表达式相同。
计算后缀表达式需要维护一个栈存储数字,从左到右扫描表达式,如果当前字符 $c$ 是数字就将其入栈,否则 $c$ 是运算符,取出栈顶的两个数字,进行运算后将结果压入栈中。最后栈中仅剩的一个数字就是后缀表达式的值。
由于要计算短路数,所以要建出表达式树,具体过程与计算后缀表达式的值相同。
建出表达式树后一次 dfs 求解,每次递归完左子树后根据左子树节点值和运算符判断是否短路即可。注意被多次使用的栈 sta 不能为 char 类型,否则 $n \geq 128$ 时会爆炸。
时间复杂度 $O(n)$。
#include<bits/stdc++.h>
using namespace std;
int n,dan,dor,top,sta[1'000'005],son[1'000'005][2];
char c[1'000'005],s[1'000'005];
int dfs(int x){
if(son[x][0]==0) return s[x]-'0';
int ret=dfs(son[x][0]);
if(s[x]=='&'){
if(ret==0) return ++dan,0;
return dfs(son[x][1]);
}
else{
if(ret==1) return ++dor,1;
return dfs(son[x][1]);
}
}
int main(){
freopen("expr.in","r",stdin);
freopen("expr.out","w",stdout);
scanf("%s",c+1);
for(int i=1;c[i]!='\0';i++){
if(isdigit(c[i])) s[++n]=c[i];
else if(c[i]=='(') sta[++top]=c[i];
else if(c[i]==')'){
while(sta[top]!='('){
s[++n]=sta[top];
--top;
}
--top;
}
else{
while(top&&sta[top]!='('&&c[i]>=sta[top]){
//char(&) < char(|)
s[++n]=sta[top];
--top;
}
sta[++top]=c[i];
}
}
while(top) s[++n]=sta[top],--top;
s[n+1]='\0';
for(int i=1;i<=n;i++){
if(isdigit(s[i])) sta[++top]=i;
else{
son[i][1]=sta[top],--top;//注意左右子树顺序
son[i][0]=sta[top],--top;
sta[++top]=i;
}
}
int ans=dfs(sta[top]);
printf("%d\n%d %d\n",ans,dan,dor);
return 0;
}