数学、组合数学

最大的难点在于发现本题是数学题。

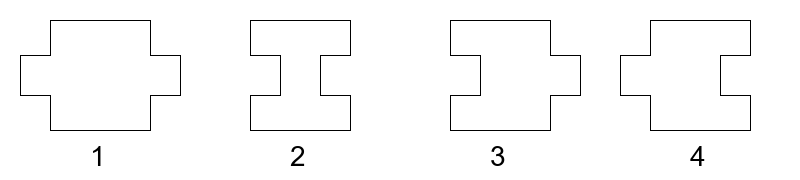
发现 $3,4$ 都只能延长 $1,2$ 的长度，在去掉所有 $3,4$ 之后图形变成了 $1,2$ 交替的形态。

那么 $1,2$ 的数量之差大于 $1$ 则没有合法图形，接下来分类讨论三种情况。

有数量相等的 $1,2$ 时若整个图形最左边的一块是 $1$，那么就有 $c_1 + 1$ 个空位可以放入 $4$（每个 $1$ 的左边都可以放任意多个，最右端的 $2$ 的右边也能放），有 $c_2$ 个空位可以放入 $3$（每个 $1$ 的右边都可以放任意多个），答案为在 $c_1 + 1$ 个空位里放入的 $c_4$ 个同样的球，空位可以不放的方案数乘上在 $c_2$ 个空位里放入 $c_3$ 个同样的球，空位可以不放的方案数。

考虑隔板法，有 $c_4$ 个球，现在要将其分割为 $c_1 + 1$ 份，每份可以为空，那么就是在 $c_1 + c_4$ 个空中选定 $c_1$ 个空表示分割。

加上整个图形最左边的一块是 $2$ 的方案数。

$$\Large{C_{c_1 + c_4}^{c_1} C_{c_2 + c_3 - 1}^{c_2 - 1} + C_{c_1 + c_4 - 1}^{c_1 - 1} C_{c_2 + c_3}^{c_2}}$$

如果 $1$ 比 $2$ 多一个，那么图形左右都得是 $1$，答案就是在 $c_1$ 个空里放 $c_4$ 个球的方案数乘上在 $c_1$ 个空里放 $c_3$ 个球的方案数。

如果 $2$ 比 $1$ 多一个，同理图形左右都得是 $2$，答案就是在 $c_2$ 个空里放 $c_3$ 个球的方案数乘上在 $c_2$ 个空里放 $c_4$ 个球的方案数。

合并这两部分，令 $n = \max(c_1,c_2)$ 再计算答案。

$$\Large{C_{n + c_3 - 1}^{n - 1} C_{n + c_4 - 1}^{n - 1}}$$

特判掉只有 $3,4$ 拼图的情况。

预处理组合数，时间复杂度 $O(n)$。

#include<bits/stdc++.h>
using namespace std;
constexpr int mod=998'244'353;
Combination<Mint<mod>,2'000'005,mod> C;
int c[8];
void solution(){
    cin>>c[1]>>c[2]>>c[3]>>c[4];
    if(c[1]==0&&c[2]==0){
        if(c[3]!=0&&c[4]!=0) cout<<0<<'\n';
        else cout<<1<<'\n';
    }
    else if(abs(c[1]-c[2])>=2){
        cout<<0<<'\n';
    }
    else if(c[1]==c[2]){
        cout<<C(c[1]+c[4],c[1])*C(c[2]+c[3]-1,c[2]-1)+C(c[1]+c[4]-1,c[1]-1)*C(c[2]+c[3],c[2])<<'\n';
    }
    else{
        int n=max(c[1],c[2]);
        cout<<C(n+c[3]-1,n-1)*C(n+c[4]-1,n-1)<<'\n';
    }
}
int T;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>T;
    while(T--) solution();
    return 0;
}