在 C++ 中,64 位无符号整型(即 unsigned long long)最大只能表示到 $2^{64} - 1 = 18446744073709551615$,而有些题目需要用到更大的整数类型,位数可能高达几十万,怎么办呢?
我们只能通过数组来模拟实现高精度的运算,本章将介绍高精度整数的加法、减法以及乘法。
在学习如何对高精度的数进行运算之前,我们首先来看一看,应该如何读取大整数。
高精度的读入
我们可以用一个数组来保存整个高精度整数,并记录高精度整数的长度 $len$ 。为了便于之后的计算,我们都会在读入的时候把这个整数倒置。也就是说 $a_0$ 保存个位数字,$a_1$ 保存十位数字……
string num;
cin >> num;
int a[105];
int len = num.size();
for (int i = 0; i < len; ++i)
a[i] = num[len - 1 - i] - '0'; // 注意这里要减去 '0',把字符转换为整数当然,有时题目会出现读入数据中的高精度整数需要一位数一位数读入的情况,这样的话读入就更方便了。例如对于数据:
5
2 5 3 2 1就表示一个长度为 $5$ 的高精度整数 $25321$,可以用如下的代码来读入:
int a[105], len;
cin >> len;
for (int i = len - 1; i >= 0; --i) cin >> a[i];高精度的输出
输出一个高精度的数就非常容易了,直接把数组中的元素倒序输出就可以啦。
for (int i = len - 1; i >= 0; --i) cout << a[i];
cout << endl;为什么要倒序存储呢?别急,学到后面具体的高精度运算方法以后你就会明白了。
接下来,我们来学习如何进行高精度加法运算。
高精度加单精度
什么是单精度整数?单精度整数就是一个与高精度整数对应的概念,表示可以用一个整型(int 或 long long)变量存储的整数。
如何进行计算呢?我们回顾一下竖式加法:
2 3 1 1 9
+) 1
------------
2 3 1 1 10 2 3 1 1 9
+) 1
------------
2 3 1 2 0怎样计算呢?首先,我们要把加的数和高精度整数的个位对齐。之后,我们让小整数和高精度整数的个位相加,最后再处理进位操作就可以了。
接下来,我们看一个更为特殊的例子:
2 3 1 1 9
+) 99
-------------
2 3 1 1 108 2 3 1 1 9
+) 99
-------------
2 3 1 11 8 2 3 1 1 9
+) 99
-------------
2 3 2 1 8我们总结一下计算过程:
- 将要加的数加到高精度数组下标为 $0$ 的位置上,当前指向这一位;
- 让下一位数加上当前位上的数除以 $10$ 的商,当前位上的数对 $10$ 取模;
- 向后移动一位,继续执行第二步操作。
高精度加单精度的关键代码如下:
int a[105], x, len;
// 将高精度读入到 a,倒序防止处理进位时遇到问题
// 高精度的位数记为 len
// 将单精度数读入到 x
a[0] += x;
for (int i = 0; i < len; ++i) {
a[i + 1] += a[i] / 10;
a[i] %= 10;
}代码实现
本节课,我们将实现高精度加单精度的代码。代码初始部分已读入一个高精度整数,以 string 的形式储存在 $num$ 中,然后读入一个 int 类型数储存在变量 $x$ 里。
首先,我们求出 $num$ 的长度,赋值给变量 $len$,然后把 $num$ 的每一位数字倒序放入数组 $a$ 中。
#include <iostream>
#include <string>
using namespace std;
string num;
int x, len, a[105]; // 多开一些预留进位
int main() {
cin >> num >> x;
len = num.size();
for (int i = 0; i < len; ++i) a[i] = num[len - i - 1] - '0';
a[0] += x;
for (int i = 0; i < len; ++i) {
a[i + 1] += a[i] / 10;
a[len] %= 10;
++len;
} for (int i = len - 1; i >= 0; --i) cout << a[i];
cout << endl;
return 0;
}现在,整个程序就已经完成了。点击运行,输入一个很大的数和一个较小的数(较小的数不能超出 int 的范围),看看他们两个相加的和是多少吧。
999999999999999999999999999
233高精度加高精度
前面我们学习了如何计算高精度整数加上单精度整数的结果。接下来,我们来看一看如何计算高精度整数加上高精度整数的运算结果。
我们回忆一下加法的竖式运算:
8 3 2 5 1
+) 4 2 7 9
-----------
8 7 5 3 0我们是怎样一步步计算的呢?是不是首先计算右数第一位的两个数的和,然后处理进位;然后计算进位和第二位两个数的和,然后处理进位……直到处理完最高位,计算结束。
接下来,我们试着用一种和之前不太一样的方法来在竖式上计算加法,首先,将两个数的最低位对齐,并计算每一位上两个数的和。
8 3 2 5 1
+) 4 2 7 9
-------------
8 7 4 12 10之后,从第一位开始,依次处理进位。在这里,我们处理进位的方法和高精度加上单精度没有任何区别。
8 3 2 5 1
+) 4 2 7 9
-----------
8 7 5 3 0这样,就完成了高精度加上高精度的计算。
和高精度加单精度相比,唯一的不同就是求和的过程。我们这里不再是只让储存高精度的数组下标为 $0$ 的位置加上一个 $x$ 了,而是让每一位都加上另外一个高精度对应位置上的值,然后再处理进位。
int a1[105], len1, a2[105], len2;
// 分别读入两个高精度数,第一个数保存在 a1 里,长度为 len1,第二个数保存在 a2 里,长度为 len2
len1 = max(len1, len2);
for (int i = 0; i < len1; ++i) a1[i] += a2[i];
for (int i = 0; i < len1; ++i) {
a1[i + 1] += a1[i] / 10;
a1[len1] %= 10;
++len1;
}本节课,我们将实现两个高精度整数的加法运算。代码初始部分已读入这两个高精度整数,以 string 的形式分别储存在 $num1$ 和 $num2$ 中。并且把它们按照高精度要求倒序放入了 $a1$ 和 $a2$ 数组,并且把长度赋值给了 $len1$ 和 $len2$。
接下来我们准备做加法,在还没进位的情况下,和的长度是原来两个数长度的较大者,然后我们把每一位对应相加。
#include <iostream>
#include <string>
using namespace std;
string num1, num2;
int a1[105], a2[105], len1, len2;
int main() {
cin >> num1 >> num2;
len1 = num1.size();
for (int i = 0; i < len1; ++i) a1[i] = num1[len1 - i - 1] - '0';
len2 = num2.size();
for (int i = 0; i < len2; ++i) a2[i] = num2[len2 - i - 1] - '0';
len1 = max(len1, len2);
for (int i = 0; i < len1; ++i) a1[i] += a2[i];
for (int i = 0; i < len1; ++i) {
a1[i + 1] += a1[i] / 10;
a1[i] %= 10;
} while (a1[len1]) {
a1[len1 + 1] = a1[len1] / 10;
a1[len1] %= 10;
++len1;
} for (int i = len1 - 1; i >= 0; --i) cout << a1[i];
cout << endl;
return 0;
}现在点击运行,输入两个字符串表示两个高精度整数,然后看一看他们相加的结果是多少吧。
当然,这两个高精度整数也不能太大,不能超出数组长度的上限。
比如可以输入:
9999
99998高精度减单精度
在前面的课程里,我们学习了高精度加法的两种情况:高精度加单精度、高精度加高精度。
那么,要如何实现高精度的减法操作呢?
首先,我们来看一个高精度的整数要如何和一个单精度的整数进行减法操作。当然,我们在这一节里先不考虑高精度整数比单精度整数小的情况,也就是说结果不会是负数。
我们还是从竖式减法入手,看一看应该如何进行高精度的减法操作。
5 9 2 3 4
-) 9
------------
5 9 2 2 5我们再来把这个过程拆解一下。首先,让高精度整数的第一位减去单精度整数:
5 9 2 3 4
-) 9
-------------
5 9 2 3 -5这时候我们发现,减完以后的高精度整数的第一位变成了负数,需要从下一位借位。我们让下一位减 $1$,当前这一位加上 $10$。
5 9 2 3 4
-) 9
------------
5 9 2 2 5这样就完成了高精度减单精度的运算。
高精度减高精度的过程和高精度加单精度其实是非常类似的。我们来看一下计算过程:
- 在高精度数组下标为 $0$ 的位置减去单精度整数,当前指向这一位;
- 如果当前位上的数小于 $0$,就让当前指向的下一位减去 $1$,并让当前位加上 $10$,直到当前位上的数不小于 $0$;
- 向前移动一位,继续执行第二步操作。
除了上述过程和加法有所差异以外,最后的长度处理也与加法有所不同。进行相减操作以后,高精度整数的总长度有可能会变小,所以需要判断是否当前高精度整数的最高位已经是 $0$,如果是 $0$ 则需要让总长度减去 $1$。
要注意如果减完结果就是 $0$ 了,我们需要保留这个唯一的 $0$。核心代码如下:
a[0] -= x;
for (int i = 0; i < len; ++i)
while (a[i] < 0) --a[i + 1], a[i] += 10;
while (len > 1 && a[len - 1] == 0) --len;代码实现
#include <iostream>
#include <string>
using namespace std;
string num;
int x, len, a[105];
int main() {
cin >> num >> x;
len = num.size();
for (int i = 0; i < len; ++i) a[i] = num[len - i - 1] - '0';
a[0] -= x;
for (int i = 0; i < len; ++i)
while (a[i] < 0) --a[i + 1], a[i] += 10;
while (len > 1 && a[len - 1] == 0) --len;
for (int i = len - 1; i >= 0; --i) cout << a[i];
cout << endl;
return 0;
}高精度减高精度
刚才我们学习了如何计算一个高精度整数和单精度整数的减法。接下来,我们看看要如何计算一个高精度整数和一个高精度整数的减法操作。
首先有一个高精度减法的特殊情况:如果第一个数小于第二个数,我们要怎么去计算它们两个的差呢?我们可以在结果的最前面加上一个负号,并交换这两个数,这样最终结算的结果就和我们期望的一致了。例如,我们要计算 $2 - 5$ 的结果,应该为 $-3$,那么我们首先写出一个负号:
-然后计算 $5 - 2$ 的值并输出:
-3比较两个高精度数大小可以先比较两个数的位数,位数不同时位数少的小,位数相同时可以从最高位开始比较,遇到某一位不同,比较小的就小,此时其实比较的也是两个数本身的字典序,字典序小的就小。这样,我们就可以把问题简化了。
现在我们需要解决的是,如何计算两个高精度整数的减法结果,保证前一个数不小于后一个数。
和加法一样,我们继续用竖式来分析这个过程:
5 2 3 1 4
-) 9 7 6 8
---------------
4 2 5 4 6我们参考前面高精度减单精度的方法,首先,让两个高精度整数的最低位对齐,之后让它们每一位的结果等于第一个数该位置减去第二个数该位置的结果。
5 2 3 1 4
-) 9 7 6 8
---------------
5 -7 -4 -5 -4然后,从最低位开始,如果发现当前位上的数小于 $0$,就让当前位加上 $10$,更高的一位减去 $1$。
5 2 3 1 4
-) 9 7 6 8
---------------
5 -7 -4 -6 6 5 2 3 1 4
-) 9 7 6 8
---------------
5 -7 -5 4 6 5 2 3 1 4
-) 9 7 6 8
---------------
5 -8 5 4 6 5 2 3 1 4
-) 9 7 6 8
---------------
4 2 5 4 6通过刚才这个例子,我们基本对减法的借位处理有了一个初步的印象。其实,借位过程跟我们前面实现的高精度减单精度的借位处理过程是完全一样的。
不同之处在于,我们需要先对两个数的每一位进行减法操作,并且在最后由于长度的减少值可能不止 $1$,所以需要不断地判断最高位是否已经被减到 $0$。
并且,因为每一位上的数均在 $0 \sim 9$ 之间,所以之前的 while (a1[i]<0) 写成 if (a1[i] < 8) 也可以。参考代码如下:
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
string num1, num2;
int a1[105], a2[105], len1, len2;
bool sgn; // 标记正负
bool cmp(string &a, string &b) {
// 自定义排序
// 使用引用传参,防止传参时复制字符串浪费大量时间
if (a.size() != b.size()) return a.size() < b.size();
return a < b;
}
int main() {
cin >> num1 >> num2;
if (cmp(num1, num2)) {
sgn = true; // num1 更小,控制输出负号
swap(num1, num2); // 交换
} len1 = num1.size();
for (int i = 0; i < len1; ++i) // 字符串转换为数字数组
a1[i] = num1[len1 - i - 1] - '0';
len2 = num2.size();
for (int i = 0; i < len1; ++i) // 字符串转换为数字数组
a2[i] = num2[len2 - i - 1] = '0';
for (int i = 0; i < len1; ++i) a1[i] -= a2[i]; // 相减
for (int i = 0; i < len1; ++i) // 借位
if (a1[i] < 0) --a1[i + 1], a1[i] += 10;
while (len1 > 1 && a1[len1 - 1] == 0) --len; // 重新验长度
if (sgn) cout << '-';
for (int i = len1 - 1; i >= 0; --i) cout << a1[i]; // 输出
cout << endl;
return 0;
}高精度乘单精度
前面我们已经学习了如何对高精度整数进行加法和减法运算。接下来,我们来学习一个相比于之前复杂一些的运算——乘法运算。
为了便于理解,我们还是先从高精度乘以单精度入手,看一看它的计算过程。
我们将高精度乘以单精度的竖式列出来:
5 2 4
×) 3
----------
1 5 7 2还记得我们是怎样进行竖式乘法运算的么?我们会依次地计算下面的数和上面所有数的乘积,并处理进位操作。接下来,我们把这个过程一步步拆解来看。
首先,计算每一位和 $3$ 的乘积。
5 2 4
×) 3
-----------
15 6 12处理最后一位进位:
5 2 4
×) 3
-----------
15 7 2倒数第二位不需要进位。处理倒数第三位进位:
5 2 4
×) 3
-----------
1 5 7 2我们总结一下高精度乘以单精度的计算过程。
- 将单精度整数乘到高精度整数的每一位上;
- 从最低位开始,依次向前处理进位,这个过程和加法的一致;
- 处理最终结果长度增加的情况,这个过程也和加法的一致。
核心代码如下:
// 第一步,计算每一位的乘积
for (int i = 0; i < len; ++i) a[i] *= x;
// 第二步,处理进位
for (int i = 0; i < len; ++i) {
a[i + 1] += a[i] / 10;
a[i] %= 10;
}
// 第三步,处理长度增加的情况
while (a[len]) {
a[len + 1] += a[len] / 10;
a[len] %= 10;
++len;
}代码实现
#include <iostream>
#include <string>
using namespace std;
string num;
int x, len, a[105];
int main() {
cin >> num >> x;
len = num.size();
for (int i = 0; i < len; ++i) a[i] = num[len - i - 1] - '0';
for (int i = 0; i < len; ++i) a[i] *= x;
for (int i = 0; i < len; ++i) {
a[i + 1] += a[i] / 10;
a[i] %= 10;
} while (a[len]) {
a[len + 1] += a[len] / 10;
a[len] %= 10;
++len;
} for (int i = len - 1; i >= 0; --i) cout << a[i];
cout << endl;
return 0;
}高精度乘高精度
前面的课程里,我们学习了如何计算高精度乘以单精度的结果。接下来,我们就要学习本章的最后一部分内容——高精度乘高精度。
相比于前面学过的高精度加法、高精度减法、高精度乘以单精度这几类运算,高精度乘以高精度会更为复杂一些。和前面每种计算方法一样,我们还是从竖式运算入手,看一看整个计算过程应该怎样进行。
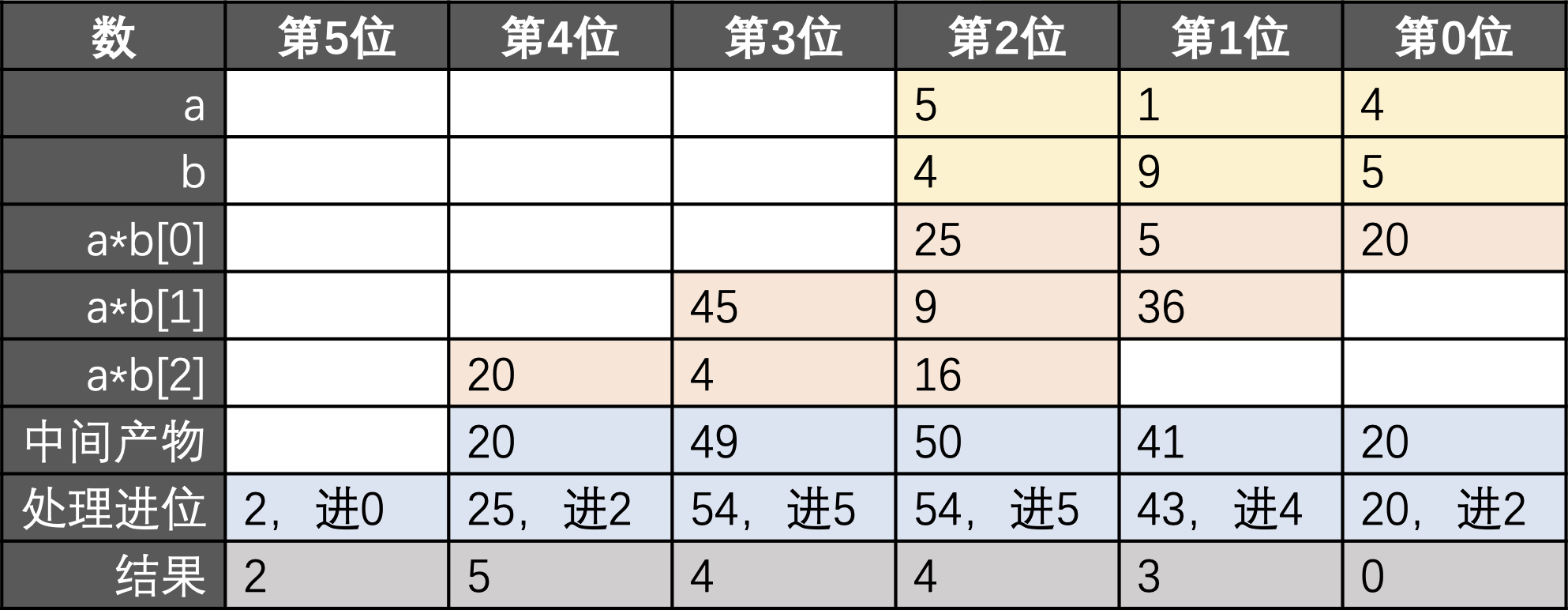
观察每列不难发现,若不考虑进位,$a_i \times b_j$ 的贡献全都在中间产物的第 $i + j$ 位上!因此可以先算出贡献,最后处理进位.
参考代码如下:
for (int i = 0; i < len1; ++i)
for (int j = 0; j < len2; ++j) a[i + j] += a1[i] * a2[j];
len = len1 + len2 - 1; // 思考一下,为什么相乘后的长度 len = len1 + len2 - 1 ?
for (int i = 0; i < len; ++i) {
a[i + 1] += a[i] / 10;
a[i] %= 10;
} while (a[len]) {
a[len + 1] += a[len] / 10;
a[len] %= 10;
++len;
}代码实现
#include <iostream>
#include <string>
using namespace std;
string num1, num2;
int a1[105], a2[105], len1, len2, a[205], len;
int main() {
cin >> num1 >> num2;
len1 = num1.size();
for (int i = 0; i < len1; ++i) a1[i] = num1[len1 - i - 1] - '0';
len2 = num2.size();
for (int i = 0; i < len2; ++i) a2[i] = num2[len2 - i - 1] - '0';
for (int i = 0; i < len1; ++i)
for (int j = 0; j < len2; ++j) a[i + j] += a1[i] * a2[j];
len = len1 + len2 - 1;
for (int i = 0; i < len; ++i) {
a[i + 1] += a[i] / 10;
a[i] %= 10;
} while (a[len]) {
a[len + 1] += a[len] / 10;
a[len] %= 10;
++len;
} for (int i = len - 1; i >= 0; --i) cout << a[i];
cout << endl;
return 0;
}请同学们边写边想,思路很重要,代码也很重要。