请注意，如无特殊说明，本文默认序列的下标从 $1$ 开始。

在现实生活中，经常需要对事物或信息进行排序。具体而言，我们收集到的数据大多是无序的，而我们需要有序的结果作为产出或作为后续步骤的输入。

有序性是一个很好的规律。例如，若一个序列是有序的，我们就可以在 $O(1)$ 时间内查找第 $k$ 小的元素，但对于无序序列就很困难。

将无序的序列转变为有序，即是排序问题。本讲义将介绍若干种排序算法。我们将会看到，不同算法均有各自适应的应用场景，并非只需掌握一种即可。

计数排序

洛谷 P1271。

学校正在选举学生会成员，有 $n$（$n \le 999$）名候选人，每名候选人编号分别从 $1$ 到 $n$，现在收集到了 $m$（ $m \le 2 \times 10^6$）张选票，每张选票都写了一个候选人编号。

现在想把这些堆积如山的选票按照投票数字从小到大排序。

输入 $n$ 和 $m$ 以及 $m$ 个选票上的数字，求出排序后的选票编号。

样例输入

2 5 2 2 5 2 2 2 1 2

样例输出

1 2 2 2 2 2 2 2 5 5

显然，题意即是经典的排序问题。输入无序序列，输出有序序列。我们可以考虑现实中如何（匿名）计票：

  1. 取出一张票（可以按照任意顺序，一般按照收集顺序即可）。
  2. 将其放入与其编号相同的票箱，且该堆的计数 $+1$。

例如上述样例，有：

1742461968623.png

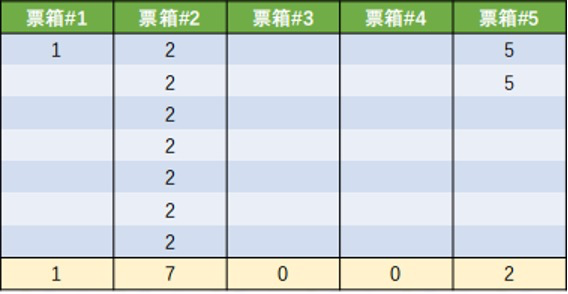
因为是匿名计票，所以选票本身的特殊性并不重要，表格中实际有效的只有总计数值。

1742461974578.png

得到有序序列，我们只需要按照票箱号从小到大从票箱中拿出选票即可。此时我们有 $1$ 张 #1、$7$ 张 #2 和 $2$ 张 #5，因此序列为：

$$ \text{1 | 2 2 2 2 2 2 2 | | | 5 5} $$

即为所求。

注意中间的隔断“$\text{|}$”：我们依然可以“尝试”从 $3$、$4$ 号票箱取票，但因为是空的，所以没有取出内容。

使用数组模拟票箱。根据刚才的结论，我们只需要记载票箱内的选票数即可。

int a[1010] = {0};

接下来，我们按照输入顺序读取每一张票，并置入票箱：

for (int i = 1; i <= m; ++i) cin >> tmp, ++a[tmp];

最后，再按照票箱编号顺序取出所有选票（为了表述清晰，我们使用循环变量 $i$ 代表选票，$j$ 代表票箱）：

for (int j = 1; j <= n; ++j)
    for (int i = 1; i <= a[j]; ++i) cout << j << ' ';

计数排序顾名思义，即统计每一个元素出现的次数，再按照顺序依次排列。数列中的元素就是“票”而一个与元素取值范围相符的数组就是“票箱”。

记 $n$ 为数列长度，$m$ 为取值范围。

需要 $O(n)$ 的时间统计每一数值出现次数。之后再用 $O(n+m)$ 的时间构造出结果数列，总时间 $O(n+m)$。另外，需要 $O(m)$ 的额外空间作为票箱。

优点：当 $m$ 较小时，时间复杂度近似于 $O(n)$，性能强大。
缺点：当 $m$ 远大于 $n$ 时，时空复杂度均取决于 $m$，得不偿失，且取值范围为非整数时，无法实现。

当原数组的数据比较集中时，才推荐使用计数排序。

计数排序的变种

  • 离散化计数排序：若能将不可表示的数据范围（双向）映射到较小的整数集合上则可以在映射后使用计数排序。这一映射过程称为离散化。
  • 桶排序：将数列按数值区间（而非具体数值）划分为若干个桶。桶内采用其他排序算法。
  • 基数排序：从低到高对每一个（$X$ 进制）位进行一次计数排序。这样，当高位有序时，所有低位均已有序。可以保证只使用X个桶。

此处不要求掌握。

基于交换的排序

现在我们开始玩牌。你要如何整理你的手牌呢?

我都是把相同的数字牌扣在桌面上来排序的！这不还是一种计数排序吗？没错，但是这样你的对手就可以通过观看牌桌上倒扣的牌堆推测你的牌型。所以你决定只通过交换的方式来排序。

首先给出一些需要掌握的前置知识——逆序对。

假设排序应当是从小到大，如果有一对牌，前面的那张牌比后面的那张牌数字大，那么我们称这两张牌是一个逆序对。形式化地，当一个序列 $a$ 中存在正整数 $i, j$ 使得 $i < j$ 且 $a_i > a_j$，那么 $\langle a_i, a_j \rangle$ 称为一个逆序对。

1742461983232.png

基于交换的排序方法

接下来我们来了解基于交换的排序方法。

所谓交换，即数列元素两两比较，若顺序反了则对换二者位置。由于每一次交换逆序对数必然减少，持续交换必然可以完成排序，且具有不用到其他变量而直接在原数列中操作、额外空间复杂度为 $O(1)$ 的优点。

考虑到元素两两间均需要互相比较，可以大致估计出，此类方法最坏时间复杂度均约为 $O(n^2)$。

选择排序

思路：$n$ 次大循环，第 $i$ 次小循环中，用小循环寻找数列中第 $i$ 小的元素。如果发现更小的数字，则交换至第 $i$ 个位置。

for (int i = 1; i <= n - 1; ++i)
    for (int j = i + 1; j <= n; ++j)
        if (a[j] < a[i]) swap(a[i], a[j]);

特点

  1. 实现简单。
  2. 每次迭代都能保证至少一个（最小）元素的位置被确定。
  3. 前 $i$ 个元素有序，且为最小的 $i$ 个元素。

1742461987556.png

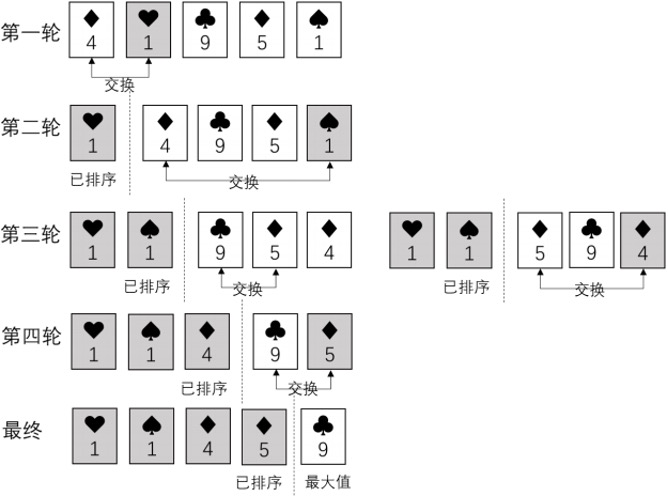
事实上，由于前 $i - 1$ 项已经排序完毕，第 $i$ 小的元素等价于第 $i$ 项至第 $n$ 项中的最小元素。

选择排序常用于 $k$ 很小时快速求解前 $k$ 大（或小）元素。

冒泡排序

思路：不超过 $n$ 次大循环，每次大循环按照顺序比较相邻元素并交换，直到序列有序。

for (int i = 1; i <= n - 1; ++i)
    for (int j = 1; j <= n - i; ++j)
        if (a[j] > a[j + 1]) swap(a[j], a[j + 1]);

特点

  1. 总交换次数恰为逆序对数。
  2. 每次迭代都能保证至少一个（最大）元素的位置被确定。
  3. 后 $i$ 个元素有序，且为最大的 $i$ 个元素。

1742461991945.png
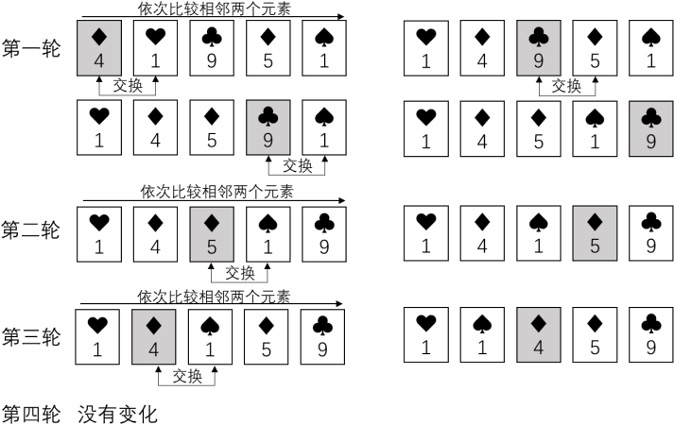
冒泡排序常用于模拟逆序对相关的问题。

插入排序

思路：$n$ 次大循环，第 $i$ 次大循环将第 $i$ 个元素向前交换，直至左侧元素不大于它，或抵达数列首部。

for (int i = 2; i <= n; ++i) {
    int cur = a[i], j;  // 记录一下待插牌，等下还要放回去
    for (j = i - 1; j >= 1; --j) {
        if (a[j] > now) a[j + 1] = a[j];
        else break;
    } a[j + 1] = cur;
}

特点

  1. 前 $i$ 个元素有序。
  2. 排序完成之前，不能保证任何一个元素的最终位置被确定，如最小元素在数列尾部的情况。

1742461995889.png

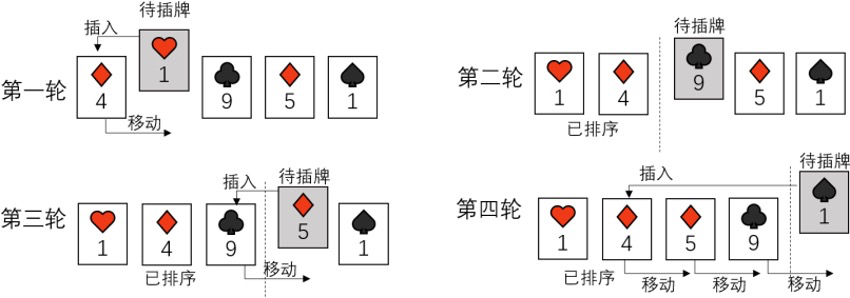
插入排序可以用来动态维护前 $k$ 大（或小）元素，单次插入时间复杂度 $O(k)$。在此场景下，第 $k + 1$ 小的元素将不会右移，而是被直接丢弃。

快速排序

是否存在性能比 $O(n^2)$ 更优的排序算法呢？答案是肯定的。

为什么基于交换的排序需要 $O(n^2)$ 时间？因为最坏情况下任意两个不同元素都需要比较，共 $\dfrac{n(n-1)}{2}$ 次。是否可以减少必须的比较次数呢？

选择排序，每一次迭代确定一个元素的位置，但是所有已确定元素均在左侧，对右侧没有指导意义。

插入排序，每一次迭代只需要与大于自身的值比较，期望只需比较一半的元素，但是没有元素确定位置，新元素的插入导致所有更大的元素右移带来额外开销。

考虑结合两者的优点，以如下数列为例：

3 8 4 10 6 7 2 5 9 1

尝试随机选取一个元素确认位置，我们称这个数为哨兵数：

3 8 4 10 *6* 7 2 5 9 1

将序列中所有比哨兵数小的数字都移动到哨兵数的左边，所有比哨兵数大的数字都移动到哨兵数的右边：

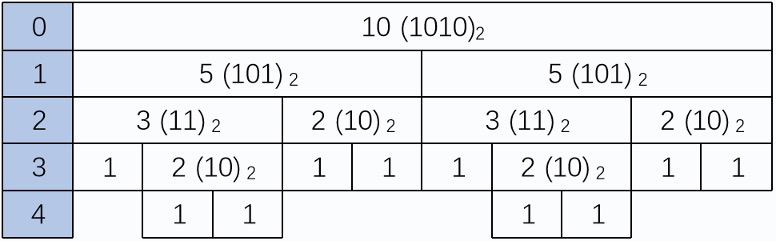
3 4 2 5 1 *6* 8 10 7 9

显然哨兵数左右两侧的元素不再需要任何比较。因此，对两侧的子数列分别采用相同的做法，直到数列不可再分（长度为 $0$ 或 $1$）。

1742462000105.png

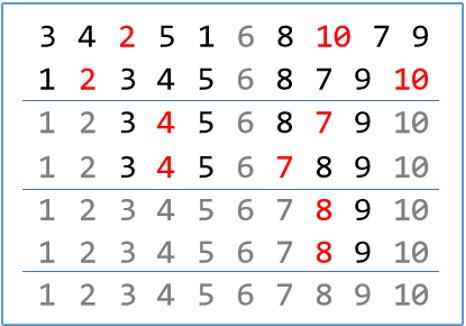
在最优情况下：每次选择的哨兵数均将数列对半分开，则 $O(\log n)$ 次划分后数列将不可再分。每次划分的复杂度为 $O(n)$，总复杂度 $O(n \log n)$。
在最坏情况下：每次选择的哨兵数均在数列一端，则退化为选择排序算法，总复杂度 $O(n^2)$。

对数

前面在复杂度中提到了 $\log n$，数学上称为 $n$ 的对数。

形式化地，若 $a^b = N$，则有 $b = \log_a N$，即幂指数 $b$ 称为“以 $a$ 为底 $N$ 的对数”，其中 $a$ 称作对数的底数，$N$ 称作对数的真数。

当 $N > 0, a > 0$ 且 $a \neq 1$ 时，有 $\log_a a^{N} = N$。此处不作证明。

因为我们每次将整个数列分为两半，上面的 $\log n$ 事实上是 $\log_2 n$。但由于大 $O$ 记号中需要省略常数，因此底数 $2$ 被略去。

如果不好理解为什么是 $\log_2 n$，我们来尝试一下感性理解。

我们可以估计对数函数的上界，将长度为 $10$ 的序列折半划分需要 $4$ 折（$10$ 的 $2$ 进制表示有 $4$ 位），所以 $\log_2 10 < 4$。

因为 $2^{31} = 2 \ 147 \ 483 \ 648$，有 $\log_2 \ 2 \ 147 \ 483 \ 648 = 31$，可见对数函数的增长十分缓慢，相比 $O(n)$ 是一个非常优秀的复杂度。

1742462006411.png

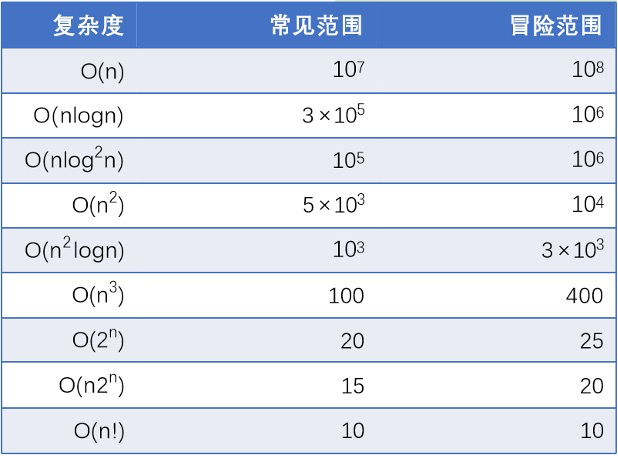
常见复杂度与数据范围

1742462012853.png

此处给出一种快速排序的实现，并不存在一种在所有情况下都最优的算法。建议自行了解，并根据应用场景选择合适的实现。

void qsort(int a[], int l, int r) {  // 引入数组的地址
    int i, j = r, flag = a[(l + r) / 2], tmp;  // flag 为哨兵
    do {
        while (a[i] < flag) ++i;  // 从左找比哨兵大的数
        while (a[j] < flag) --j;  // 从右找比哨兵大的数
        if (i <= j) {
            swap(a[i], a[j]);
            ++i, --j;
        }
    } while (i <= j);
    // 习惯上，上面用于分段的过程一般称作 partition
    if (l < j) qsort(a, l, j);
    if (r > i) qsort(a, i, r);
}

快速排序是一种基于分治法的排序算法，大多数基于分治法的算法均具有 $O(n \log n)$ 的时间复杂度。其余具有此复杂度的排序算法还有：

  1. 基数排序：基于按位处理。
  2. 归并排序：基于分治法。
  3. 堆排序：基于数据结构。

排序算法的应用

养兵千日，用兵一时。排序作为重要的算法工具，可以将无序变有序，使问题更好的得到处理。

STL 中的排序算法

algorithm（算法）库中包含很多常用的算法，包括排序。

引入头文件：

#include <algorithm>

使用排序功能：

sort(a.begin(), a.end());  // O(n log n)
sort(a.begin(), a.end(), cmp);  // O(n log n)

begin 和 end 被称为迭代器，表示需要排序位置的首末。cmp 是一个可选参数，应该作为函数名称出现，可以自定义排序的比较方法。

STL 中还有一个常用的函数，即查找函数。

find(a.begin(), a.end(), val);  // O(n), 查找

其中，$val$ 是需要查找的值。这个函数返回第一个匹配的元素的地址（即迭代器），若元素不存在则返回 a.end()。

排序以后，可以使用以下函数：

unique(a.begin(), a.end());  // O(n), 去重

我们之后会学到一个新的容器 vector。我们假设需要使长度为 $n$ 的 vector $v$ 等价到数组 $a$，那么有：

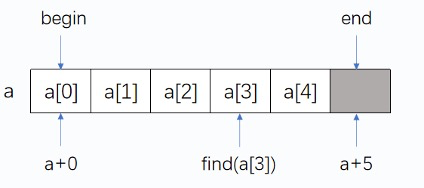
  1. a（或 a + 0）$\iff$ v.begin()。
  2. a + n $\iff$ v.end()。
  3. a + n - 1 $\iff$ v.back()，即最后一个元素。
  4. v.end() - v.begin() $\iff$ $n$。
  5. find(a[x]) - a $\iff$ find(v[x]) - v.begin() $\iff$ $x$。
  6. STL 函数的调用方法：
    1742462023221.png

1742462027303.png

洛谷 P1059。

给出 $N$（$N \le 100$）个 $1$ 到 $1000$ 的数字，输出去重后剩余数字的个数，以及去重排序后的序列。

样例输入

10
20 40 32 67 40 20 89 300 400 15

样例输出

8
15 20 32 40 67 89 300 400

解法 #1：注意到数据范围很小，可以使用计数排序。
解法 #2：直接使用 STL 中的排序、去重函数：

sort(a + 1, a + n + 1);
int cnt = unique(a + 1, a + n + 1) - a - 1;
cout << cnt << endl;
for (int i = 1; i <= cnt; ++i) cout << a[i] << ' ';

自定义排序

如果我想排序，但不是从小到大排序，怎么办？或者，能对结构体元素进行排序吗？

sort() 函数可以增加第三个参数 cmp ，也就是自定义排序的基准。cmp 函数需要两个待排序的元素 $x$、 $y$ 作为参数。返回一个 bool 值，表示 $x$ 是否严格小于 $y$。

例如实现整数从大到小排序：

bool cmp(int x, int y) {
    return x > y;
}

sort(a, a + n, cmp);

cmp 函数名称可以任取，保持上下一致即可。

洛谷 P1093。

给出 $n$（$n \le 300$）名学生的语文、数学、 英语成绩，这些学生的学号依次是从 $1$ 到 $n$。需要对这些学生进行排序。

如果总分相同，则语文分数高者名次靠前；如果语文成绩还是一样的，学号小者靠前。输出排名前 $5$ 的学生学号和总分。

样例输入

6
90 67 89
87 66 91
78 89 91
88 99 77
67 89 64
78 89 98

样例输出

6 265
4 264
3 258
2 244
1 237

可以使用 STL 进行排序。

构造一个结构体 student 用于存储学生的各项有用的信息（数学和英语并不重要，可以不存下来）。注意使用 cmp 来进行比较，当两个学生比较时，排名比较高的学生返回 true。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 310;
int n;
struct student{
    int id, chinese, total;
} a[N];

bool cmp(student a, student b) {
    if (a.total != b.total) return a.total < b.total;  // 总分先定胜负
    if (a.chinese != b.chinese) return a.chinese < b.chinese;  // 然后比语文
    return a.id < b.id;  // 最后比学号
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        int math, english;
        cin >> a[i].chinese >> math >> english;
        a[i].total = a[i].chinese + math + english;
        a[i].id = i;
    } sort(a + 1, a + n + 1, cmp);
    for (int i = 1; i <= 5; ++i) cout << a[i].id << ' ' << a[i].total << endl;
    return 0;
}

还有参照选择排序和插入排序思路的其它解法，参见课本 P139。

最后修改：2025 年 03 月 20 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏