算法的世界高深莫测，但是很多问题的解决方法简单而粗暴枚举出所有可能的情况，然后判断或者统计，从而解决问题。在很多程序设计比赛中，有许多比较简单的题目是可以通过枚举暴力解决的；而有的更具有挑战性的题目虽然有更巧妙的解法，但依然可以使用枚举，暴力地完成部分任务。
本文将介绍一些枚举与暴力策略，这是非常基础而且重要的，但是对初学者来说还是会有一些挑战。请务必理解本章之前的所有知识后再开始本章的学习。
枚举就是根据提出的问题，一一列出该问题的所有可能的解，并在逐一列出的过程中，检验每个可能解是否是问题的真正解，如果是就采纳这个解，如果不是就继续判断下一个。
枚举法一般比较直观，容易理解，但由于要检查所有的可能解，因此运行效率较低。能够用枚举法解决的题目往往是最简单的一类题目。这种题目具有以下特点：
- 枚举范围是有穷的。
- 检验条件是确定的。
验证复杂的程序的正确性，可写功能一致的暴力对照程序，并构造小规模输入数据，比较二者输出。这一过程称作对拍，在赛场上是非常实用的查错技巧。
算法问题的分类
一般而言，算法问题可以分为两类。
模拟问题
构造具体描述，使用计算机还原现实规则。
每一步的行为大多是简单而确定的，只需按照既定指示行动。
常基于数据结构，优化单步操作的复杂度。
求解问题
在全部的可能性中，搜索可行或最优解。
解是不确定的，需要枚举 / 遍历 / 检索以尝试所有可能性。
常使用迭代、搜索等算法求解，优化主要为记忆化、剪枝。
循环枚举
循环是最简单的枚举方案。
我们将基于几个例题，讲解循环枚举的思路，并简介几种优化：
- 基于数学的优化。
- 基于剪枝的优化。
- 技巧：打表法。
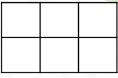
有一个 $n \times m$（$n,m \le 5000$）的棋盘，求其方格包含多少个（四边平行于坐标轴的）正方形和长方形。本题中，长方形中不包括正方形。
样例输入
2 3样例输出
8 10样例解释
如图，正方形一共 $8$ 个，长方形 $10$ 个。正方形中，边长为 $1$ 的 $6$ 个，边长为 $2$ 的 $2$ 个；长方形中，$1 \times 2$ 的 $4$ 个，$1 \times 3$ 的 $2$ 个，$2 \times 1$ 的 $3$ 个，$2 \times 3$ 的 $1$ 个。
四个参数可以确定一个长方形：左下顶点坐标 $(x_1, y_1)$ 和右上顶点坐标 $(x_2, y_2)$，也可以理解为“左右下上” $(x_1, x_2, y_1, y_2)$。
思路 0：用四重循环，直接枚举 $4$ 个参数，即两横边两竖边。
int rectangle = 0, square = 0;
for (int x1 = 1; x1 <= n; ++x1)
for (int y1 = 1; y1 <= m; ++y1)
for (int x2 = x1 + 1; x2 <= n; ++x2) // x2 从 x1 + 1 起，不重复不遗漏
for (int y2 = y1 + 1; y2 <= m; ++y2) { // 同上
if (x2 - x1 == y2 - y1) ++square; // 正方形，两边长相等
else ++rectangle; // 长方形
}为什么是 $x_2$ 从 $x_1 + 1$ 开始，$y_2$ 从 $y_1 + 1$ 开始枚举？
- 如果 $x_1 > x_2$，那么 $x_1$ 就不再是左侧了，$x_2$ 才是左侧（左图）。
- 如果 $x_1 = x_2$，那么无法构成长方形，退化为一根线段（中图）。
- 只有 $x_1 < x_2$ 才能正常构成长方形（右图）。
$y_1$ 和 $y_2$ 同理。
所以，这样可以保证不重复地遍历所有的方形。根据循环的范围可知，我们也没有遗漏任何的方形，时间复杂度 $O(n^2 m^2)$——似乎有点慢，但是至少答案正确了。
为了减少枚举量，可以考虑拆解问题，尝试解决简单问题，例如，固定其中一个顶点为 $(x, y)$，计算长方形与正方形的个数。
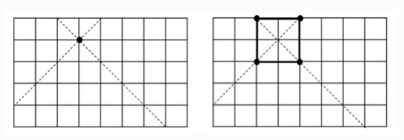
思路 1：以上图中的点 $(3, 4)$ 为例（左下角为原点），位于同一对角线（图中虚线）上所有点均可构成正方形。除自身所在行列外，所有其它点均可与其构成长方形，故直接得长方形数为 $n \times m - 正方形数$。从右图可以看出，每一个长方形或正方形均被其 $4$ 个顶点各计算一次，因此，最终答案需要除以 $4$。
斜线上的格点个数为多少呢？若顶点在长方形顶点，格点个数为长方形的短边长，即 $\min \{n, m\}$。
否则，以顶点为界分为 $4$ 份。每份都这样计算，得到正方形个数为 $\min \{x, y\} + \min \{n - x, y\} + \min \{x, m - y\} + \min\{n - x, m - y\}$。因此，枚举 $(x, y)$ 后，可在 $O(1)$ 时间内计算答案，求和。总时间复杂度 $O(nm)$，直接优化掉一个 $O(nm)$。
能否更快？
思路 2：每一个长方形重复了 $4$ 次，能否不重复呢？结合思路 0 可知，只需考虑右上角为 $(x, y)$ 的情况，因此计算斜线上的顶点时，只需要向左下角一个方向扩展。先算 $4$ 个方向，再除以 $4$，可谓是画蛇添足啊。
for (int x = 1; x <= n; ++x)
for (int y = 1; y <= m; ++y) {
int tmp = min(x, y);
square += tmp, rectangle += x * y - tmp;
}当然，这里选择固定其它角也是等价的，但是固定右上角最简单。注意：这里的原点是在左下角，列是 $x$，行是 $y$。如果选择左上角作为原点，那么枚举的就是长方形右下角。
思路 3：枚举边长 $(a, b)$。题目变为在 $n \times m$ 的长方形中能放置多少个 $a \times b$ 的方形。注意 $a, b$ 有序，即 $a \times b$ 和 $b \times a$ 不等价。
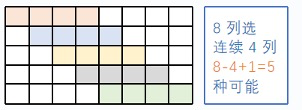
$n$ 列中选连续 $a$ 列有 $[1, a], [2, a + 1], \cdots , [n - a + 1, n]$，共 $n - a + 1$ 种可能；$m$ 列中选连续 $b$ 行构成方形，同理有 $m - b + 1$ 种情况。所以 $n \times m$ 的长方形中可容纳 $(n - a + 1) \times (m - b + 1)$ 个 $a \times b$ 的方形。
根据上面的算法，我们知道想要容纳 $a \times b$ 的方形需要两步：确定 $a$ 和确定 $b$。对于每个 $a$，有 $n - a + 1$ 种方案；对于每个 $b$，有 $m - b + 1$ 种方案，因此总的方案数是 $(n - a + 1) \times (m - b + 1)$。
也就是说，我们只需要将确定 $a$ 的方案数和确定 $b$ 的方案数乘起来，就可以得到总的方案数了。
那么，如果步骤更多，总方案数仍然等于所有步骤的方案数的乘积吗？
答案是肯定的。因此，我们有：
- 乘法原理：完成一个工程需要分 $n$ 个步骤，$a_i$（$1 \le i \le n$）代表第 $i$ 个步骤的不同方法数目，那么完成这件事共有 $S = \prod \limits_{i = 1}^{n} a_i = a_1 \times a_2 \times \cdots \times a_n$ 种不同的方法。
类似地，还有：
- 加法原理：完成一个工程可以有 $n$ 类办法，$a_i$（$1 \le i \le n$）代表第 $i$ 类方法的数目，那么完成这件事共有 $S = \sum \limits_{i = 1}^{n} = a_1 + a_2 + \cdots + a_n$ 种不同的方法。
上述两种定理构成了组合数学的基石，我们将在几周后系统性地学习组合数学。乘法原理与加法原理极其容易混淆，请各位仔细甄别。
for (int a = 1; a <= n; ++a)
for (int b = 1; b <= m; ++b) {
if (a == b) square += (n - a + 1) * (m - b + 1);
else rectangle += (n - a + 1) * (m - b + 1);
}只有长等于宽，才能构成正方形；其余均为长方形。因此，如果 $a = b$，就计入正方形。使用循环枚举 $a, b$，累加求和即可。
思路 4：沿用刚才乘法原理的思想，枚举量还可进一步减少。在 $n \times m$ 的长方形中方形个数，等价于在 $m + 1$ 条行线中选首尾 $2$ 行，在 $n + 1$ 条列线中选首尾 $2$ 列所围成的方形数目。
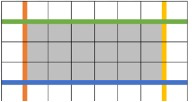
在 $n + 1$ 条列线中选 $2$ 条围长方形，左列线有 $n + 1$ 种情况；右列线不能和左列线重复，只有 $n$ 种情况。将它们乘起来。
由于重复统计（“左右”和“右左”），还要将乘积除以 $2$，因此列线的组合有 $\dfrac{n \times (n + 1)}{2}$ 种可能。
同理，行线的组合有 $\dfrac{m \times (m + 1)}{2}$ 种可能，所以一共有 $\dfrac{n \times (n + 1) \times m \times (m + 1)}{4}$ 个方形。借助思路 3，去掉其中的正方形。时间复杂度降到 $O(\min \{n, m\})$。
烤鸡时需要加入 $10$ 种配料，每种配料可放 $1$ 到 $3$ 克。美味程度是所有配料质量之和。给出一个美味程度 $n$（$n \le 5000$）按照字典序输出配料搭配的方案数量和所有的搭配方案。如果 $n$ 超过 $30$ 请输出 $0$。
样例输入
11样例输出
10 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1
思路 1：由于这题要求输出所有的具体方案，所以公式不管用了，那就硬着头皮写暴力枚举吧。首先，每一种调料至少为 $1$，所以必有 $n \ge 10$。同样，每一种调料最多为 $3$，所以必有 $n \le 30$。——共有 $10$ 种调料，所以 $10$ 重循环即可解决。
for (int a = 1; a <= 3; ++a)
for (int b = 1; b <= 3; ++b)
for (int c = 1; c <= 3; ++c)
for (int d = 1; d <= 3; ++d)
for (int e = 1; e <= 3; ++e)
for (int f = 1; f <= 3; ++f)
for (int g = 1; g <= 3; ++g)
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
if (a + b + c + d + e + f + g + h + i + j == n)
++ans;
cout << ans << endl;
for (int a = 1; a <= 3; ++a)
for (int b = 1; b <= 3; ++b)
for (int c = 1; c <= 3; ++c)
for (int d = 1; d <= 3; ++d)
for (int e = 1; e <= 3; ++e)
for (int f = 1; f <= 3; ++f)
for (int g = 1; g <= 3; ++g)
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
if (a + b + c + d + e + f + g + h + i + j == n)
cout << a << ' ' << b << ' ' << c << ' ' <<
d << ' ' << e << ' ' << f << ' ' << g <<
' ' << h << ' ' << i << ' ' << j << endl;太丑陋了。
不过，不能上公式，不代表不能用其他方法优化了。
思路 2：如果 $a + b + c + d + e$ 已经超过 $n$，那么 $f, g, h, i, j$ 无论如何取值，都不可能使得答案再等于 $n$ 了。因为 $f, g, h, i, j$ 至少取 $1$，所以 $a + b + c + d + e$ 达到 $n - 3$ 或以上的时候，就已经没有任何的可能性了。
基于上述事实，可以构造出剪枝算法：限定每一个数的范围。
for (int a = max(1, n - 27); i <= min(3, n - 9); ++a)
for (int b = max(1, n - 24 - a); i <= min(3, n - 8 - a); ++b)
for (int c = max(1, n - 21 - a - b); i <= min(3, n - 7 - a - b); ++c)
for (int d = max(1, n - 18 - a - b - c);
i <= min(3, n - 6 - a - b - c); ++d)
for (int e = max(1, n - 15 - a - b - c - d);
i <= min(3, n - 5 - a - b - c - d); ++e)
for (int f = max(1, n - 12 - a - b - c - d - e);
i <= min(3, n - 4 - a - b - c - d - e); ++f)
for (int g = max(1, n - 9 - a - b - c - d - e - f);
i <= min(3, n - 3 - a - b - c - d - e - f); ++g)
for (int h = max(1, n - 6 - a - b - c -
d - e - f - g); i <= min(3, n - 2 -
a - b - c - d - e - f - g); ++h)
for (int i = max(1, n - 3 - a - b - c - d -
e - f - g - h); i <= min(3, n - 1 - a -
b - c - d - e - f - g - h); ++i)
for (int j = max(1, n - a - b - c - d - e -
f - g - h - i); i <= min(3, n - a - b -
c - d - e - f - g - h - i); ++j) {
li[ans][1] = a;
li[ans][2] = b;
li[ans][3] = c;
li[ans][4] = d;
li[ans][5] = e;
li[ans][6] = f;
li[ans][7] = g;
li[ans][8] = h;
li[ans][9] = i;
li[ans][10] = j;
++ans;
}虽然更丑陋了。但是效率更高了，赢！
将 $1, 2, \cdots, 9$ 共 $9$ 个数分成三组，分别组成三个三位数，且使这三个三位数的比例是 $A : B : C$（ $A < B < C < 10^9$），试求出所有满足条件的三个三位数，若无解，输出 $\tt{No!!!}$。
样例输入
1 2 3样例输出
192 384 576 219 438 657 273 546 819 327 654 981
已知只要枚举第一个三位数，从 $123$ 枚举到 $987$。就可以根据比例确定另两个（不一定存在）最后检验得到的结果是否总共同时具有 $9$ 个不同数位。
bool b[10];
long long a, b, c, x, y, z, cnt; // 全局变量 cnt 自动初始化为 0
void go(int x) { // 分解三位数到桶里
b[x % 10] = true;
b[x / 10 % 10] = true;
b[x / 100] = true;
}
bool check(int x, int y, int z) {
memset(b, 0, sizeof(b));
if (y > 999 || z > 999) return false;
go(x), go(y), go(z);
for (int i = 1; i <= 9; ++i) if (!b[i]) return false;
return true;
}
int main() {
cin >> a >> b >> c;
for (x = 123; x <= 987; ++x) {
if (x * b % a || x * c % a) continue;
y = x * b / a, z = x & c / a;
if (check(x, y, z)) cout << x << ' ' << y << ' ' << z << endl, ++cnt;
} if (!cnt) cout << "No!!!" << endl;
return 0;
}子集枚举
有时候问题可以归纳为这样一个情况：在若干元素当中，选择其中一些以达成特定条件。
我们可以像“烤鸡”一题中那样，将每一个元素视为有两种情况：选或不选。然后使用多重循环解决问题。
对于这种特殊的问题，可以使用子集枚举。
注意到每一个元素只有两种状态。联想到二进制。用第 $i$ 个二进制位来表达第 $i$ 个元素的取舍。习惯上，$1$ 表示选取，$0$ 表示丢弃。那么一个 $n$ 位二进制整数就可以表达 $n$ 个元素的取舍，即：
- $25 = $
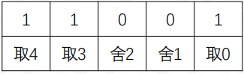$= \{0, 3, 4\}$。
请思考：为什么二进制的最右边的一位，代表第一个元素呢？
可用 C++ 自带的位运算符，轻松实现集合的各项运算。
上表中出现了新的运算符，用于操作一个整数中的二进制位，我们称其为位运算符。常见位运算符有以下几种：
- 按位与：用符号
&表示，a & b表示将 $a$ 与 $b$ 的每一个二进制位都进行与运算，即两个数位均为 $1$ 时结果为 $1$，否则为 $0$。数学上写作 $\text{and}$。- 按位或：用符号
|表示，a | b表示将 $a$ 与 $b$ 的每一个二进制位都进行或运算，即两个数位均为 $0$ 时结果为 $0$，否则为 $1$，数学上写作 $\text{or}$。- 按位异或：用符号
^表示，a ^ b表示将 $a$ 与 $b$ 的每一个二进制位都进行异或运算，即两个数位不同时结果为 $1$，否则为 $0$，数学上写作 $\text{xor}$。- 按位非：用符号
~表示，~a表示将 $a$ 的每一个二进制位都进行取反运算，即当前位为 $1$ 时改为 $0$，当前位为 $0$ 时改为 $1$，数学上写作 $\text{not}$。- 左移：用符号
<<表示，a << b表示将 $a$ 的二进制位全部向左移动 $b$ 位。- 右移：用符号
>>表示，a >> b表示将 $b$ 的二进制位全部向右移动 $b$ 位。位运算符的优先级非常低，也就是说，在语句中常常是先进行其他运算，再进行位运算，因此一定要勤加括号。
这种二进制表示法又称状态压缩。之后还会深入学习一种基于状态压缩的算法——状态压缩动态规划。
有了二进制表示后，就可以通过 for 循环遍历 $0$（全 $0$，即空集）到 $2n - 1$（全 $1$，即全集）的所有整数，得到所有可能的子集。
int u = 1 << n; // u = 2 ^ n, u - 1 即为全集
for (int s = 0; s < u; ++s) // 枚举所有子集 [0, u)
if (/* 满足题设条件 */) {
// 进行统计
}优点：非常简单方便，集合运算可以基于整数运算 $O(1)$ 实现。
限制：元素个数不能太多。一般不超过 $20$ 个。
从 $n$（$n \le 20$）个整数中任选 $k$ 个整数相加，求有多少种选择情况可以使和为质数。
样例输入
4 3 3 7 12 9样例输出
1样例解释
选 $3 + 7 + 19 = 29$，一共只有一种。
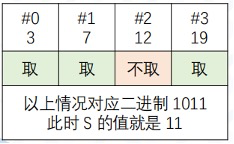
进行子集枚举之后，求和做质数判定。题目要求选 $k$ 个整数，且和为质数。所以判定条件就是：
- 二进制表示中恰好包含 $k$ 个 $1$。
- 将对应元素取出后，使用质数判定算法发现是质数。
bool eval(unsigned int s) {
int sum = 0;
for (int i = 0; i < n; ++i)
if (s & (1 << i)) sum += a[i]; // 如果第 i 个元素在 s 中，求和
return is_prime(sum); // 质数判定
}
unsigned int u = 1 << n; // u = 2 ^ n, u - 1 即为全集
for (unsigned int s = 0; s < u; ++s) // 枚举所有子集 [0, u)
if (__builtin_popcount(s) == k && eval(s)) // 恰好包含 k 个 1 且通过质数判定
++ans; // 统计上述代码中出现了一个新的数据类型
unsigned int，表示无符号整数。不同于int，unsigned int的最高位也代表一个数值位（int的最高位是符号位，$0$ 为正数，$1$ 为负数），因此unsigned int总是表示一个非负数，范围在 $[0, 2^{32} - 1]$ 之间。还有一个新的函数
__builtin_popcount()，是 GCC 编译器提供的内置函数，用于计算一个无符号整数的二进制表示中 $1$ 的个数。例如，__builtin_popcount(x)表示计算无符号整数 $x$ 的二进制表示中 $1$ 的个数。事实上，
__builtin_popcount()函数只能计算无符号整数，但现代编译器通常选择将有符号整数转为无符号整数，然后再进行调用。因此，上面的代码中如果将变量 $s$ 以int类型定义，也不会影响最终的结果，但为了保证教学代码的规范，此处使用unsigned int。
排列枚举
给定 $n$（$1 \le n \le 9$），输出自然数 $1$ 到 $n$ 所有不重复的排列，即 $n$ 的全排列。所谓全排列，指将 $1 \sim n$ 所有数字不重复、不遗漏地构成数列的所有可能情况。要求按字典序输出。
样例输入
3样例输出
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
第一个排列当然是 $1, 2, 3, \cdots , n$。如何生成第二个排列呢？
我们通常使用的十进制数，可以认为是一种特殊的排列：允许各位数字可以相同。在十进制中，生成下一个排列等价于 $+1$。
十进制数如何处理 $+1$ 呢？可以近似写作如下算法：
- 令当前位为最低位。
- 令当前位 $+1$。
- 如果结果为 $10$，则产生进位，当前位前移，转到第 2 步。否则结束。
再回到全排列。全排列要求每一项都必须不同，所以可以理解为每一次 $+1$ 都会产生进位。于是问题就变为，需要进多少位？
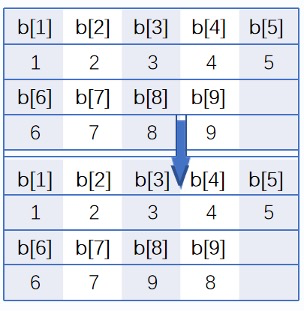
进位之后，高位仍然是可以保证不变的。
而进位则需要将当前位 $p$ 替换为后缀中大于 $p$ 的最小值 $q$。如下图：
其中 $p$ 是大于 $q$ 的最小元素。于是得到代码：
bool next_permutation(int a[], int n) {
int p, q;
for (p = n - 1; p >= 1 && a[p] > a[p + 1]; --p); // 寻找单调递减后缀
if (p <= 0) return false; // 已经是最后一个排列了
for (int i = p + 1, j = n; i <= j; ++i, --j) swap(a[i], a[j]); // 翻转单调递减后缀为递增
for (int i = p + 1; i <= n; ++i) if (a[i] > a[p]) { // 找到最小大于 p 的值
q = i;
break;
} swap(a[p], a[q]);
return true; // 生成了新的排列
}其实万能的 STL 里面也是有这个算法的。
#include <algorithm> // 头文件
bool next_permutation(begin, end); // 函数原型和大多数 STL 函数一样，begin 指数组首地址，end 指数组末地址 $+1$。
do {
for (int i = 1; i <= n; ++i) cout << a[i] << ' ';
cout << endl;
} while (next_permutation(a + 1, a + n + 1));单次调用 next_permutation() 的时间复杂度为 $O(n)$，一共有 $O(n!)$ 个可能的排列，总复杂度为 $O(n \times n!)$。
对于本题而言，这个复杂度是可以接受的。对于其他问题而言，一定要根据题目需要，设计合适的剪枝算法。
洛谷 P1618（是的上面已经出现过一次了）。
将 $1, 2, \cdots, 9$ 共 $9$ 个数分成三组，分别组成三个三位数，且使这三个三位数的比例是 $A : B : C$（ $A < B < C < 10^9$），试求出所有满足条件的三个三位数，若无解，输出 $\tt{No!!!}$。
样例输入
1 2 3样例输出
192 384 576 219 438 657 273 546 819 327 654 981
这里给出另外一种解法：直接枚举三个三位数再检验，每次变排列。
for (int i = 1; i <= 9; ++i) a[i] = i;
do {
x = a[1] * 100 + a[2] * 10 + a[3];
y = a[4] * 100 + a[5] * 10 + a[6];
z = a[7] * 100 + a[8] * 10 + a[9];
if (x * b == y * a && y * c == z * b)
cout << x << ' ' << y << ' ' << z << endl, ++cnt;
} while (next_permutation(a + 1, a + 10));
if (!cnt) cout << "No!!!" << endl;总结
- 求解问题：在若干种选项中，寻找可行解或最优解的问题。
- 暴力枚举：遍历所有选项解决求解问题的手段。
- 循环枚举：数学优化，剪枝优化，打表法。
- 子集枚举：二进制状态压缩，
__builtin_popcount()。 - 排列枚举：排列生成算法，
next_permutation()。
学而时习之，不亦说乎。学而不思则罔，思而不学则殆。