请注意,如无特殊说明,本文默认序列的下标从 $1$ 开始。
我们先来看一个简单的例子:
你现在有面值为 $20$ 元、$10$ 元、$5$ 元、$1$ 元的纸币足够张,现在想用最少张数的纸币支付 $58$ 元。最差的方法是支付 $58$ 张 $1$ 元的纸币,但我相信你肯定不会这么做。你会按下面的步骤想:
- $20$ 元纸币用 $2$ 张,还需凑 $18$ 元。
- $10$ 元纸币用 $1$ 张,还需凑 $8$ 元。
- $5$ 元纸币用 $1$ 张,还需凑 $3$ 元。
- $1$ 元纸币用 $3$ 张,刚好凑出了 $58$ 元,一共用了 $7$ 张纸币。
即优先用大面值的纸币,能用多少就用多少,然后再一步步考虑小面值,这其实就是一种贪心的思想。像这种贪心是显而易见的,也不难证明其正确性,而有些贪心结论却隐藏得很深。
求解最优化问题的算法通常需要经过一系列的步骤,在每个步骤都面临多种选择。这类问题我们可以采用贪心思想来解决,我们在每一步都做出当前看起来最正确的决定,这些决定组合起来,就可以得到整个问题的最优解,即通过做出局部最优选择来构造全局最优解。
还有一种算法叫做动态规划(Dynamic Programming, DP),常用于处理那些不适用贪心的最优化问题,我们将在之后学习这部分内容。
下面,我们通过几个例子,由浅入深地带领大家学习贪心算法。
马上又到了一年一度的新年联欢,小明作为班里的班长,负责组织策划新年联欢活动,他决定采购一些奖品奖励积极参与每个项目活动的同学。为了激励更多的人参与活动,需要采购的奖品数目越多越好。班费中可支出的钱数为 m元,现给定商店中几种可作为奖品的物品的价格和库存数量,怎样才能购得最多的物品数?
输入格式
输入共 $n + 1$ 行:
第一行包含两个正整数 $m$($1 < m < 10^4$)和 $n$($1 < n < 100$),表示可支出的费用为 $m$ 元和可供购买的物品有 $n$ 种。
接下来 $n$ 行,每行包含两个数(以空格分隔),分别表示一种物品的单价 $a_i$ 和库存数量 $b_i$。保证 $a_i, b_i \le 1000$。
输出格式
输出一行一个整数,表示最多可以购买的物品数量。
样例输入
500 6 100 3 20 15 50 10 35 5 5 6 60 2样例输出
25样例解释
价格为 $5$ 的可以买 $6$ 个,价格为 $20$ 的可以买 $15$ 个,价格为 $35$ 的可以买 $4$ 个,总共 $25$ 个奖品。
本题的贪心结论很简单:我们只需按单价从小到大排序,每次尽可能地买单价低的物品。因为每购买一件物品,我们都希望剩余的钱更多。
从这里可以看出,贪心就是人的一种本质思想,在现实中你也会优先选择更便宜的。本题的核心代码如下:
const int N = 110;
struct node {
int x, y; // x 表示价格,y 表示个数
} a[N];
bool cmp(node p1, node p2) { // 结构体排序函数
return p1.x < p2.x;
}
sort(a + 1, a + n + 1, cmp);
int ans = 0;
for (int i = 1; i <= n; ++i) {
int t = min(m / a[i].x, a[i].y); // 剩余的钱最多可以买多少个 a[i]
m -= a[i].x * t;
ans += t;
}哈利波特在与伏地魔的战斗中毁坏了自己的魔杖,于是他决定去奥利凡德的魔杖店买个新的。他在店里看到几个魔杖和几个盒子,每个魔杖的长度为 $X_1, X_2, \cdots, X_n$,每个盒子的长度为 $Y_1, Y_2, \cdots, Y_n$。一个长度为 $X$ 的魔杖能放进长度为 $Y$ 的盒子里,当且仅当 $X \le Y$。
哈利想知道他能否把所有魔杖都放进盒子里,并且每个盒子只能放一根魔杖。请你帮他解决这个问题。
输入格式
第一行一个整数 $n$($1 \le n < 100$),表示魔杖的数量。
第二行 $n$ 个整数 $X_i$($1 \le X_i < 10^9$),表示每根魔杖的长度。
第三行 $n$ 个整数 $Y_i$($1 \le Y_i < 10^9$),表示每个盒子的长度。
输出格式
如果哈利能把所有魔杖放进盒子里,输出 $\texttt{DA}$,否则输出 $\texttt{NE}$。
样例输入
3 7 9 5 6 13 10样例输出
DA
先尝试把最长的魔杖的放进最长的盒子里,然后尝试把第二长的魔杖放进第二长的盒子里……最后尝试把最短的魔杖放进最短的盒子里。
显然这样就一定是最优配对了,如果这种方法都无法实现,更别说其他的放法了。参考代码:
sort(a + 1, a + n + 1); // 给盒子排序
sort(b + 1, b + n + 1); // 给魔杖排序
bool ok = true;
for (int i = 1; i <= n; ++i) if (a[i] > b[i]) {
ok = false;
break;
} if (ok) cout << "DA" << endl;
else cout << "NE" << endl;有 $n$($1 \le n \le 1000$)个人在一个水龙头前排队接水,假如每个人接水的时间为 $T_i$,请编程找出这几个人排队的一种顺序,使得几个人的平均等待时间最小。
输入格式
第一行为一个整数 $n$。
第二行 $n$ 个整数,第 $i$ 个表示第 $i$ 个人的节水时间 $T_i$。
输出格式
输出文件有两行,第一行为一种平均时间最短的排队顺序;第二行为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。
样例输入
10 56 12 1 99 1000 234 33 55 99 812样例输出
3 2 7 8 1 4 9 6 10 5 291.90
我们的贪心策略是:让接水时间少的人先接水。参考代码:
#include <iostream>
#include <algorithm>
#include <iomanip>
using namespace std;
const int N = 1010;
int n;
double sum;
struct water {
int num, time;
} p[N];
bool cmp(water a, water b) {
if (a.time != b.time) return a.time < b.time;
return a.num < b.num;
}
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> p[i].time;
p[i].num = i;
} sort(p + 1, p + n + 1, cmp);
for (int i = 1; i <= n; ++i) {
cout << p[i].num << ' ';
sum += i * p[n - i].time;
} cout << endl;
cout << fixed << setprecision(2) << sum / n << endl; // 输出保留两位小数
return 0;
}Farmer John 最近为奶牛们的图书馆添置了一个巨大的书架,尽管它是如此的大,但它还是几乎瞬间就被各种各样的书塞满了。现在,只有书架的顶上还留有一点空间。
所有 $N$($1< N < 20,000$)头奶牛都有一个确定的身高 $H_i$($1 < H_i < 10,000$)。设所有奶牛身高的和为 $S$,书架的高度为 $B$,并且保证 $1 \le B \le S < 2,000,000,007$。
为了够到比最高的那头奶牛还要高的书架顶,奶牛们不得不像演杂技一般,一头站在另一头的背上,叠成一座“奶牛塔”。当然,这个塔的高度,就是塔中所有奶牛的身高之和。为了往书架顶上放东西,所有奶牛的身高和必须不小于书架的高度。显然,塔中的奶牛数目越多,整座塔就越不稳定,于是奶牛们希望在能够到书架顶的前提下,让塔中奶牛的数目尽量少。
现在,奶牛们找到了你,希望你帮她们计算这个最小的数目。
输入格式
从文件 shelf.in 读入。
第 $1$ 行有两个用空格隔开的整数 $N$ 和 $B$。
第 $2$ 到第 $N + 1$ 行,每行有一个整数,表示 $H_i$。
输出格式
输出到文件 shelf.out。
输出一行一个整数,即最少要多少头奶牛叠成塔,才能够到书架顶部。
样例输入
6 40 6 18 11 13 19 11样例输出
3样例解释
一共有 $6$ 头奶牛,书架的高度为 $40$,奶牛们的身高在 $[6, 19]$ 之间。一种只用 $3$ 头奶牛就达到高度 $40$ 的方法为 $18 + 11 + 13$。当然还有其他方法,此处省略。
贪心策略是什么?显然地,为了保证奶牛数量尽可能少,我们需要选择尽可能高的奶牛。
本题中出现了“从文件读入”和“输出到文件”的字样,这意味着我们不能再像之前一样在控制台里操作了(就是运行之后弹出的黑色窗口),而是在文件中完成输入和输出操作。
我们可以将文件 shelf.in 和 shelf.out 放到源代码文件的同一目录下,然后在主函数开头加入以下语句来实现对样例文件的输入与输出:
freopen("shelf.in", "r", stdin);
freopen("shelf.out", "w", stdout);其中,shelf.in 与 shelf.out 为文件名。上述代码表示从 shelf.in 文件中读取数据,并将结果输出到 shelf.out 文件中。
如果目录下没有 shelf.out 文件,那么程序会自动创建它,并且将输出写入其中。但提交时,仍然仅需要提交这份代码,不需要提交输入输出文件。
通常情况下,比赛中会为你提供几组大样例,样例文件中包含后缀名为 .in 的输入文件与 .ans 的答案文件。你可以将输出的 .out 文件与后缀名为 .ans 的样例文件比较,以达到调试程序的目的。
我们将参加的 CSP-J/S 和后续的 NOIP 比赛中也将使用这样的输入输出方式,所以请确保完全理解这部分内容。
参考代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20010;
int n, m, a[N];
int main() {
freopen("shelf.in", "r", stdin);
freopen("shelf.out", "w", stdout);
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> a[i];
sort(a + 1, a + n + 1);
for (int i = n; i; --i) {
m -= a[i];
if (m <= 0) {
cout << n - i + 1 << endl;
break;
}
} return 0;
}番茄君在奶茶店打工,他把几个杯子排成一行,然后随意地往里面加上珍珠,已知第 $i$ 个杯子的珍珠数目是 $a_i$。突然他想起来老板让他少用珍珠,必须满足相邻两个杯子里的珍珠数目不超过 $m$。现在他只能把多余的珍珠去掉,放回冰箱里(没错,就是这么不卫生)。请你帮他计算下,最少需要去掉多少珍珠。
输入格式
从文件 tea.in 读入。
第一行两个整数 $n, m$($2 \le n \le 10^5, 1 \le m \le 10^9$)。
第二行 $n$ 个整数,表示初始时每个杯子里的珍珠数目 $a_i$($1 \le a_i \le 10^9$)。
输出格式
输出到文件 tea.out。
输出一个整数,表示最少需要去掉的珍珠数目。
样例 #1 输入
3 10 7 8 10样例 #1 输入
8样例 #2 输入
3 10 15 1 10样例 #2 输出
6
参考代码如下:
#include <iostream>
using namespace std;
const int N = 1e5 + 10; // 1e5 表示 1 乘 10 的 5 次方
int n, m, a[N];
long long ans;
int main() {
freopen("tea.in", "r", stdin);
freopen("tea.out", "w", stdout);
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 2; i <= n; ++i) if (a[i] + a[i - 1] > m) {
ans += a[i] + a[i - 1] - m;
a[i] = max(0, m - a[i - 1]);
} cout << ans << endl;
return 0;
}在某次膜拜大会上,一些神牛被要求集体膜拜。这些神牛被奖励每人吃一些神牛果。但是,每个神牛的肚量不一样。为了不显得某些人吃得太多,决定两人一组,使得吃得最多的那组吃得尽量少。
输入格式
第一行一个偶数 $n$($n \le 10^4$)。
第二行有 $n$ 个正整数,为给定的一列数字,表示每个神牛能吃多少神牛果。数字均小于 $10^9$。
输出格式
输出一个正整数,表示吃的最多的一组神牛吃的个数的最小值。
样例输入
4 1 5 2 8样例输出
9
遇事不决先排序,我们首先会把所有整数从小到大排序,排序后的结果为 $a_1, a_2, \cdots, a_n$。
当 $n=2$ 时,只有一种分配方案,答案为 $a_1 + a_2$。
当 $n = 4$ 时,有 $3$ 种分配方案:
- $a_1 + a_2$ 和 $a_3 + a_4$,显然后者更大。
- $a_1 + a_3$ 和 $a_2 + a_4$,显然后者更大。
- $a_1 + a_4$ 和 $a_2 + a_3$。
容易发现,前两种方案都比较浪费,可以通过适当的调整更优。而第三种方案,无论 $a_1 + a_4$ 还是 $a_2 + a_3$ 更大,都比前两种方案小。
那么就能想到贪心策略是每次用最小的和最大的来配对,即 $(a_1, a_n), (a_2, a_{n - 1}), \cdots, (a_{\tfrac{n}{2}}, a_{\tfrac{n}{2}} + 1)$,然后答案就为其中的最大值。
在坐标轴上有几条线段,每条线段的左端点为 $x_i$,右端点为 $y_i$。现在你需要删去部分线段,使得剩下的线段除端点外无公共部分。请你计算最多能保留的线段数目。
输入格式
第一行一个整数 $n$($1 \le n \le 10^6$),表示线段的条数。
接下来 $n$ 行,每行两个整数 $x_i, y_i$($0 \le x_i < y_i \le 10^6$)。
输出格式
一个整数,表示最多能保留的线段数。
样例输入
6 6 8 3 6 4 7 1 4 7 9 0 5样例输出
3
首先我们会想到一种贪心策略:优先选择长度较短的区间。容易举出反例:
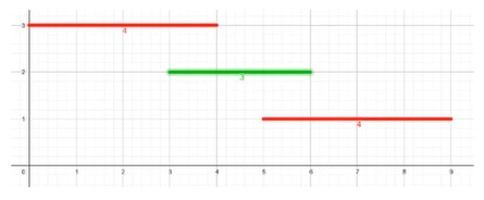
如果刚开始选了绿色线段就没法选其他线段了,而更优的方法是选择红色线段。所以这种贪心策略是错误的。我们又想到第二种贪心策略:把左端点从小到大排序,从左到右一条条覆盖,记录一下当前已经覆盖到的最右边位置,然后每次插入左端点大于该位置且左端点最小的线段。
依然能举出反例:
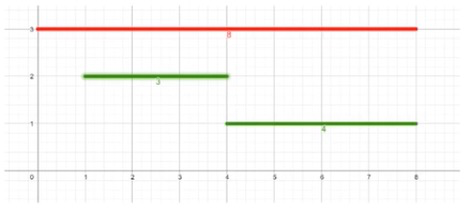
红色线段的左端点最小,但是实在太长了,选了它就没法选别的线段了,不如选两条绿色线段。所以这种贪心策略也是错误的。
那么我们就想到第三种贪心策略:把右端点从小到大排序,从左到右一条条覆盖,记录一下当前已经覆盖到的最右边位置,然后每次插入左端点大于该位置且右端点最小的线段。这种贪心策略是正确的,因为我们的目的就是让所选的线段尽可能早的结束,这样能给予更多的空间来选择剩余的线段。
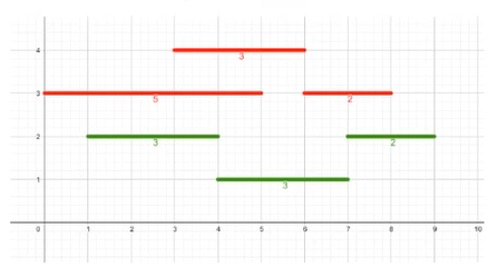
如上图所示,我们会选择三条绿色线段。参考代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
int n, ans, now; // now 用于记录右端位置
struct node {
int x, y;
} a[N];
bool cmp(node p1, node p2) {
return p1.y < p2.y;
}
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i].x >> a[i].y;
sort(a + 1, a + n + 1, cmp);
for (int pos = 1; pos <= n; ++pos) if (a[pos].x >= now) {
now = a[pos].y;
++ans;
} cout << ans << endl;
return 0;
}同一个问题,可能有多种贪心策略。贪心选择性质是:全局最优解可以通过局部最优选择来达到。
有 $N$ 组学生,给出初始时每组中的学生个数,再给出每组学生人数的上界 $R$ 和下界 $L$($L \le R$),每次你可以在某组中选出一个学生把他安排到另外一组中,问最少要多少次才可以让 $N$ 组学生的人数都在 $[L, R]$ 中。
输入格式
第一行一个整数 $N$($1 \le N \le 50$),表示学生组数。
第二行 $N$ 个整数,表示每组的学生个数 $a_i$。
第三行两个整数 $L, R$,表示下界和上界。保证 $1 \le a_i, L, R \le 1000$。
输出格式
一个整数,表示最少的交换次数,如果不能满足题目条件输出 $-1$。
样例输入
3 1 5 10 4 7样例输出
3
参考代码如下:
#include <iostream>
using namespace std;
const int N = 60;
int n, a[N], l, r, sum, ans1, ans2;
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i], sum += a[i];
cin >> l >> r;
if (sum >= l * n && sum <= r * n) {
for (int i = 1; i <= n; ++i) { // 人数越多的越往少的里面加
if (a[i] < l) ans1 += l - a[i]; // 少的补人
if (a[i] > r) ans2 += a[i] - r;
} cout << max(ans1, ans2) << endl;
} else cout << -1 << endl;
return 0;
}由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要。帮助 Marry 乳业找到最优的牛奶采购方案。
Marry 乳业从一些奶农手中采购牛奶,并且每一位奶农为乳制品加工企业提供的价格是不同的。此外,就像每头奶牛每天只能挤出固定数量的奶,每位奶农每天能提供的牛奶数量是一定的。每天 Marry 乳业可以从奶农手中采购到小于或者等于奶农最大产量的整数数量的牛奶。
给出 Marry 乳业每天对牛奶的需求量,还有每位奶农提供的牛奶单价和产量。计算采购足够数量的牛奶所需的最小花费。
注:每天所有奶农的总产量大于 Marry 乳业的需求量,
输入格式
第一行两个整数 $N$($1 \le N < 2, 000, 000$)和 $M$($1 \le M < 5, 000$)是提供牛奶的农民个数。
接下来 $M$ 行,每行两个整数 $p_i$($0 \le p_i \le 1000$)和 $x_i$($1 \le x_i \le 100$),分别表示农民 $i$ 的牛奶的单价与产量。
输出格式
单独的一行包含单独的一个整数,表示 Marry 的牛奶制造公司拿到所需的牛奶所要的最小费用。
参考代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010;
int n, m, ans;
struct node {
int p, x;
} a[N];
bool cmp(node p1, node p2) {
return p1.p < p2.p;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> a[i].p >> a[i].x;
sort(a + 1, a + m + 1, cmp);
for (int i = 1; i <= m; ++i) {
int t = min(a[i].x, n);
ans += t * a[i].p;
n -= t;
if (n == 0) break;
} cout << ans << endl;
return 0;
}