请注意,如无特殊说明,本文默认序列的下标从 $1$ 开始。
线性查找
查找就是在给定数据中找到目标数据。
比如给一个数组,找到其中等于 $x$ 的数,大于 $x$ 的数,小于 $x$ 的数,大于等于 $x$ 并且小于等于 $y$ 的数的数量、位置等,都是查找算法可以解决的问题。
最简单的查找算法就是直接用 for 循环扫描一遍数组,看每一个数,找到想要的数,或者统计想要的结果。
比如有多少个数等于 $x$ 就可以写成:
for (int i = 1; i <= n; ++i)
if (a[i] == x) ++cnt;找到第一个 $x$ 的位置就可以写成:
int p = -1;
for (int i = 1; i <= n; ++i)
if (a[i] == x) {
p = i;
break;
}找出符合要求的数
这一节我们来通过线性查找统计有多少个大于等于 $l$ 并且小于等于 $r$ 的数。
相关的输入输出已经做好了,我们只需要进行统计。用 for 循环看数组的每一位。
#include <iostream>
using namespace std;
int a[1005];
int main() {
int n, l, r, cnt = 0;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
if (a[i] >= l && a[i] <= r) ++cnt;
} cout << cnt << endl;
return 0;
}二分查找
二分查找(Binary Search)也称折半查找,它是一种效率较高的查找方法。
先从一个例子感受下二分这种思想的魅力:
小张在心中想了一个在 $[1, 1000]$ 范围内的整数,她考验小李能否在 $10$ 次机会内猜出来。小李每次会猜一个数,并且能够得到小张的三个回复:太小了、太大了,猜中了。
那么采用二分的思想,小李第一个猜的数会是 $500$,他会根据小张的回复进行第二次猜数:
- 猜中了,游戏结束。
- 太大了,那么说明范围在 $1 \sim 499$ 以内,于是小李下次猜 $250$。
- 太小了,那么说明范围在 $501 \sim 1000$,于是小李下次猜 $750$。
这样小李每次猜不中的时候都会把范围缩小一半,而 $\log_2 1000 < 10$,因此 $10$ 次以内一定能够猜出来。
二分查找最常见的一类问题是:在一个有序、无重复元素的数组中找出某个关键字。比如现在有一个包含 $n$ 个元素的递增数组,想要在其中找到元素 $x$。
我们会把 $n$ 个元素分成大致相等的两部分,取 $a_{\frac{n}{2}}$ 与 $x$ 做比较。
- 如果 $x = a_{\frac{n}{2}}$,则找到 $x$ 算法中止。
- 如果 $x < a_{\frac{n}{2}}$,则只要在数组 $a$ 的左半部分继续查找 $x$。
- 如果 $x > a_{\frac{n}{2}}$,则只要在数组 $a$ 的右半部分继续查找 $x$。
二分查找的算法要求
- 必须采用顺序存储结构(支持随机访问),比如数组,
vector(上节学过)。 - 必须按关键字大小有序排列。
二分查找的过程
下面我们用一个具体例子来说明二分查找算法过程。在这个例子中,我们要从 $1$,$3$,$5$,$7$,$10$,$12$,$14$ 中找出关键字 $12$。
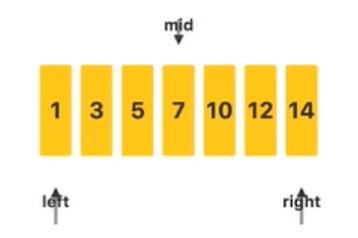
首先,用三个值来标记数组的待查找区间的左端点 $left$、右端点 $right$ 和中间位置 $mid$。
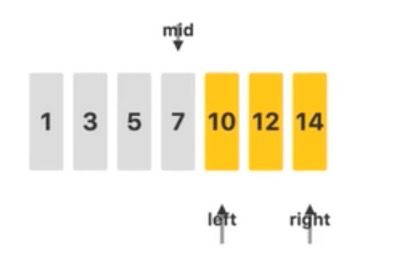
我们发现,中间位置 $mid$ 指向的值 $7 < 12$,因此,要找的元素一定在 $mid$ 的右边。于是我们将左端点 $left$ 修改为 $mid + 1$,继续后面的查找过程。
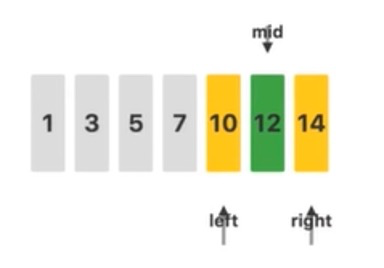
此时,更新 $mid$,发现 $mid$ 指向的值就是我们要找的 $12$,二分查找结束。这里的 $mid$ 一般取 $\left \lfloor \dfrac{l + r}{2} \right \rfloor$。(有没有更好的表示方法?)
如果关键字并没有在数组中出现,整个查找的过程是怎样的呢?我们还是用上面给出的数据 1 3 5 7 10 12 14 作为例子。
要在其中查找关键字 $11$,和之前一样,先确定三个标记的位置。
接下来,判断待查关键字 $11$ 和 $mid$ 指向的值的关系,发现 $11 > 7$,去右侧继续查询:
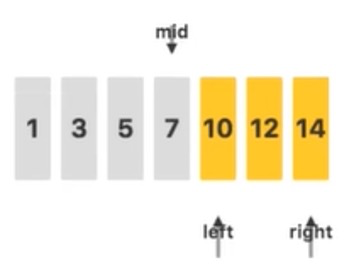
接下来,判断待查关键字 $11$ 和 $mid$ 指向的值的关系,发现 $11 < 12$,去左侧继续查询:
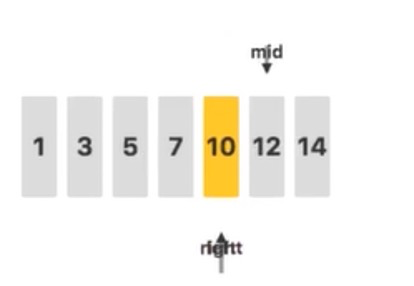
接下来,判断待查关键字 $11$ 和 $mid$ 指向的值的关系,发现 $11 > 10$,去右侧继续查询:
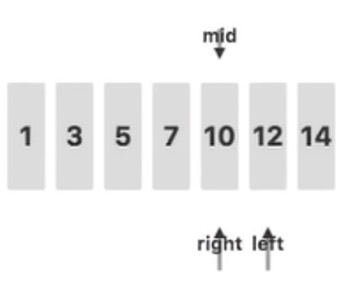
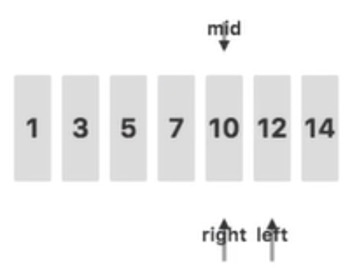
此时,由于 $left$ 比 $right$ 更大,说明没有找到关键字 $11$,查询结束。
二分查找的步骤
- $x = a_{mid}$: 找到,结束查找
- $x < a_{mid}$:在 $[left, mid - 1]$ 中继续査找 $x$。
- $x > a_{mid}$:在 $[mid + 1, right]$ 中继续査找。
- 如此重复进行,直到查找成功或范围缩小为空 $(left > right)$ 即查找不成功为止。
比较次数
给定一个数组 $a$ 为 $\{1, 2, 3, 5, 8, 13\}$,其中数组下标从 $0$ 开始,使用二分查找看 $10$ 在不在数组中。刚开始 $left = 0$,$right = 5$,每次取 $mid$ 为 $\left \lfloor \dfrac{left + right}{2} \right \rfloor$,需要看 $3$ 次不同的 $mid$ 才能完成查找。
binary_search()
在 C++ 中,我们可以很方便地使用 sort() 对一个数组进行排序,而不需要写出很长的排序算法的程序。那么,我们能不能用简单现成的函数来实现对一个数组的二分查找呢?
答案是肯定的。在 C++ 中,我们可以用 binary_search() 对一个数组进行二分查找。不过,在使用 binary_search() 之前,我们应该先引入 algorithm 头文件。
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int a[] = {1, 2, 3, 4, 5, 7, 9};
cout << binary_search(a, a + 7, 3) << endl;
cout << binary_search(a, a + 7, -5) << endl;
cout << binary_search(a, a + 7, 5) << endl;
cout << binary_search(a, a + 7, 2) << endl;
cout << binary_search(a, a + 7, 10) << endl;
return 0;
}和 sort() 的用法比较类似,binary_search() 一共有三个参数,其中前两个参数表示查找的区间,a 和 a+7 表示从 $a_0$ 到 $a_6$ 进行查找。
这点与 sort() 类似, binary_search(a + l, a + r, x) 是在 $a_l$ 到 $a_{r - 1}$ 中进行查找。 binary_search() 的最后一个参数表示要查找的元素值。
在进行二分查找前,需要保证待查找的部分是从小到大有序的,一般情况下可以先将整个数组从小到大排序。数组中有重复元素不影响查找。
函数的返回值为 bool 类型,当返回 true 时,表示在数组中找到了这个值,否则表示没找到这个值。
注意,如果 $a$ 是一个 vector,需要使用 .begin() 和 .end(),即 binary_search(a.begin(), a.end(), x),或者 binary_search(a.begin() + l, a.begin() + r, x)。
使用 binary_search()
有 $n$ 个数,$q$ 次询问,每次要查找的数是 $x$。
#include <iostream>
#include <algorithm>
using namespace std;
int n, x, q, a[1005];
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
sort(a + 1, a + n + 1);
cin >> q;
while (q--) {
cin >> x;
if (binary_search(a + 1, a + n + 1, x)) cout << "Yes" << endl;
else cout << "No" << endl;
} return 0;
}lower_bound() 与 upper_bound()
在很多情况下,我们不仅仅要判断一个值是否在有序数组中出现,例如对于如下的数组:
1 2 2 3 4 4 4 4 5 6 7 9 9 10我们有如下的两个问题:
- 找出第一个出现的 $4$ 的位置。
- 找出第一个比 $4$ 大的位置。
用 binary_search() 是肯定解决不了的,那么,是否有对应的函数来帮我们解决这两个问题呢?
在 C++ 里,还有两个非常好用的函数:lower_bound() 和 upper_bound(),它们也在头文件 algorithm 里。其中,lower_bound() 返回第一个大于等于要查找的元素值的位置,upper_bound() 返回第一个大于要查找的元素值的位置。它的参数和 binary_search() 类似,也是三个,首位置,尾位置和要查找的元素,不过返回值是找到的相应元素的位置。
lower_bound() 意思是“下界”,在这里是说这个数出现的位置最靠前也就是这个位置了,也就是第一个大于等于这个数的位置。upper_bound() 意思是“上界”,在这里是说这个数出现的位置不能在这个位置及以后了,也就是第一个大于这个数的位置。
这两个函数也要求数组是升序的。例如,假设这是一个数组 $a$(下标从 $1$ 开始),那么对于函数 upper_bound(a + 1, a + 15, 4) 和 lower_bound(a + 1, a + 15, 4) 的示意如下:
1 2 2 3 4 4 4 4 5 6 7 9 9 10
^ upper_bound
^ lower_bound因为返回值是位置,所以想要得到数组下标需要减掉数组首位置,所以 upper_bound(a + 1, a + 15, 4) - a 的值为 $9$,也就是会找到上面数组中的第一个 $5$;而 lower_bound(a, a + 14, 4) - a 的值为 $5$,也就是会找到上面数组中的第一个 $4$。如果没有找到,返回的位置为查找区间的尾位置,比如这里就是 a + 15 这个位置。这种情况在实际使用的时候可能需要特判。
在 vector 中要相应使用 .begin() 和 .end(),比如 lower_bound(a.begin(), a.end(), x) - a.begin()。
如果想要找到最后一个小于查找值的数或者最后一个小于等于查找值的数呢?还是看刚才的例子:
1 2 2 3 4 4 4 4 5 6 7 9 9 10
* ^ upper_bound
* ^ lower_bound这回想要的是就是两个标了 * 的位置,发现:
- 最后一个小于等于查找值的数的位置就是
upper_bound()的位置往前一位。 - 最后一个小于查找值的数的位置就是
lower_bound()的位置往前一位。
所以使用 lower_bound() 或者 upper_bound() 以后,算出下标再减 $1$ 就可以了。特别注意如果函数返回的就是首位置,那就说明没有小于或小于等于查找数的元素,需要特判。
使用 lower_bound() 和 upper_bound()
我们来在数组中找到大于等于 $x$ 的最小的数和大于 $x$ 的最小的数。不过要注意,如果没有找到结果,函数返回的是尾位置,这里会是 a + n + 1,算出来的 $p1$ 的值是 $n + 1$,这个需要特判。
如果 $p1 \neq n$ 就输出 $a_{p1}$,否则输出 $\texttt{No}$ 输出以后换行。
#include <iostream>
#include <algorithm>
using namespace std;
int n, x, p1, p2, a[1005];
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
sort(a + 1, a + n + 1);
cin >> x;
p1 = lower_bound(a + 1, a + n + 1, x) - a;
p2 = upper_bound(a + 1, a + n + 1, x) - a;
if (p1 != n + 1) cout << a[p1] << endl;
else cout << "No" << endl;
if (p2 != n + 1) cout << a[p2] << endl;
else cout << "No" << endl;
return 0;
}提示
- 有一个从小到大排好的序的下标为 $1$ 到 $n - 1$ 的升序数组 $a$,想要知道其中元素 $x$ 的数量,可以使用
upper_bound(a + 1, a + n + 1, x) - lower_bound(a + 1, a + n + 1, x)。- 使用
binary_search()函数时数组待查找部分必须是从小到大排序的。
练习
小张给出若干个整数,询问是否有一对数的和等于给定的数。
输入格式
共三行。
第一行是整数 $n$($1 \le n \le 10^5$),表示有 $n$ 个整数。
第二行是 $n$ 个整数,保证整数的范围在 $[0, 2 \times 10^8]$ 之间。
第三行是一个整数 $m$($0 \le m \le 2^{30}$),表示需要得到的和。
输出格式
若存在和为 $m$ 的数对,输出这两个整数,小的在前,大的在后,中间用单个空格隔开。若有多个数对满足条件,选择数对中较小的数更小的。若找不到符合要求的数对,输出一行 $\texttt{No}$。
#include <iostream>
#include <algorithm>
using namespace std;
int n, m, num[100005];
bool f;
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
cin >> m;
sort(num + 1, num + n + 1);
for (int i = 1; i <= n; ++i)
if (binary_search(num + i + 2, num + n + 1, m - num[i])) {
cout << num[i] << ' ' << m - num[i] << endl;
f = true;
break;
}
if (!f) cout << "No" << endl;
return 0;
}事实上,仍然存在比上述代码更优的算法。但此处代码用于练习 binary_search() 的使用,故不做要求。二分答案
二分思想不仅可以在有序序列中快速查询元素,还能高效率地解决一些具有单调性判定的问题。
事实上, 二分查找的本质,就是在寻找一个满足 $a_{mid} \ge k$ 这一 条件的最小的 $mid$。由于 $a$ 数组的单调性,我们设计出了这一算法。
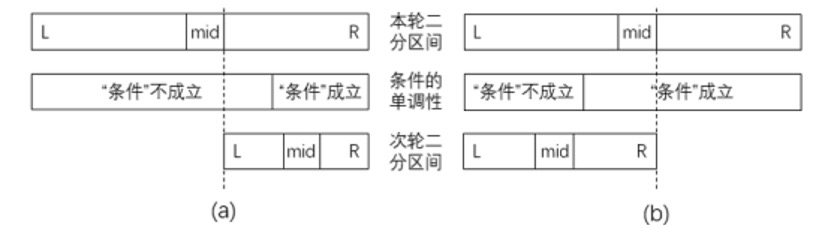
事实上,在一些具有单调性判定的问题中,我们也可以采用类似方法求解。
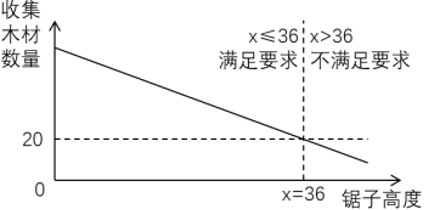
$N$ 棵树高度分别为 $a_1 \cdots a_N$,对于一个砍树高度 $H$, 可以锯下并收集到每棵树上比 $H$ 高的部分的木材。求最大的整数高度 $H$, 使得能够收集到长度为 $M$ 的木材。其中 $N \le 10^6$, 树高不超过 $10^9$。
样例输入
5 20 4 42 40 26 46样例输出
36
在样例中,每棵树的高度分别是 $\{4, 42, 40, 26, 46\}$,需要将锯子的高度调整为 $36$,这样可以分别锯下 $\{6, 4, 10\}$ 高度的木材。如果锯子高度再高一点就不能满足要求了。
先来变换一下题目:令“条件”表示“当砍树高度为 $x$ 时可以获取不少于 $M$ 的木材”,那么就是要找最大的 $x$ 使得“条件”成立。
显然,这一条件是存在单调性的。斧头高度越低,则砍下时,收获的木头越多。即然如此,就可以采用二分的思路来寻找这个数。
int find(int l, int r) { // 使用前确保答案在 [l, r] 内
int ans, mid;
while (l <= r) { // 闭区间上的二分结束条件
int mid = (l + r) / 2;
if (check(mid)) // 条件成立
ans = mid, r = mid - 1;
// 这里只需要记录满足条件的 mid,最后循环一定会结束,也一定会在 ans 中保留正确的答案
else l = mid + 1;
} return ans;
}接下来,我们的问题就改变为如何判断给定的 $x$ 是否能使条件成立(即 check() 函数)。
当砍树高度为 $x$ 时,对于某棵树,如果其高度高于 $x$,则砍去高于 $x$ 的部分,否则舍弃,就能统计处砍掉的高度。接着将砍去的高度求和,再与 $M$ 相比即可。
bool check(int h) { // 当砍树高度为 h 时能否得到大于 m 的木材
long long tot = 0;
for (int i = 1; i <= n; ++i) if (a[i] > h) tot += a[i] - h; // 按照题意模拟
return tot >= m;
}
需要注意的是,这里的 $r$ 的初始值应当大于等于所有树中最高者的高度,否则可能无法通过二分的到正确的结果。
判断条件是否成立的算法复杂度是 $O(n)$,而二分答案本身的算法度复杂度是 $O(\log A)$ ,其中 $A$ 是指最高的高度,因此总复杂度是 $O(n \log A)$。
通过本题 ,我们可以得到使用二分答案的条件:
- 命题可以被归纳为找到使得某命题
check(x)成立(或不成立)的最大(或最小)的 $x$。 - 把
check(x)看做一个值为真或假的函数,那么它一定在某个分界线的一侧全为真,另一侧全为假。 - 可以找到一个复杂度优秀的算法来检验
check(x)的真假。
通俗来讲,二分答案可以用来处理形如“最大值最小”或“最小值最大”的问题。