本文中将涉及一个新的专用术语——合法。这里的合法指的并非“符合法律”,而是“符合规则、符合条件”之意。之后我们提到“合法”一词,也都是这个意思。
我们已经学习过了暴力枚举算法——枚举出所有可能的情况,然后判断或者统计,从而解决问题。然而,枚举全部元素的效率如同愚公移山,无法应对数据范围稍大的情形,有时甚至连编写代码都很困难。
此时,我们就需要引入一个新的算法了——搜索。此搜索非彼搜索,与百度等联网搜索引擎无关。
$n$ 元组是指由 $n$ 个元素组成的序列。例如 $(1,1,2)$ 是一个三元组、$(233,254,277,123)$ 是一个四元组。
给定 $n$ 和 $k$,请按字典序输出全体 $n$ 元组,其中元组内的元素是在 $[1, k]$ 之间的整数。$1 \le n\leq 5, 1 \le k\leq 4$。字典序是指优先按照第一个元素从小到大的顺序,若第一个元素相同,则按第二个元素从小到大……依此类推。
看到这题,我们肯定会有一个最朴素的想法是:写 $k$ 层 for 循环,直接枚举所有可能的元组。代码可能是这样的:
#include <iostream>
using namespace std;
int n, m;
int main() {
cin >> n >> m;
if (n == 1)
for (int i = 1; i <= m; i++) cout << i << '\n';
else if (n == 2)
for (int i = 1; i <= m; i++)
for (int j = 1; j <= m; j++)
cout << i << ' ' << j << '\n';
else if (n == 3)
for (int i = 1; i <= m; i++)
for (int j = 1; j <= m; j++)
for (int k = 1; k <= m; k++)
cout << i << ' ' << j << ' ' << k << '\n';
else if (n == 4)
for (int i = 1; i <= m; i++)
for (int j = 1; j <= m; j++)
for (int k = 1; k <= m; k++)
for (int g = 1; g <= m; g++)
cout << i << ' ' << j << ' ' << k << ' ' << g << '\n';
else for (int i = 1; i <= m; i++)
for (int j = 1; j <= m; j++)
for (int k = 1; k <= m; k++)
for (int g = 1; g <= m; g++)
for (int h = 1; h <= m; h++)
cout << i << ' ' << j << ' ' << k << ' ' << g << ' ' << h << '\n';
return 0;
}太丑陋了。
另外,我们发现这里的 $k$ 不是固定值,因此如果直接使用循环的话,我们需要对每一个 $k$ 都写 $k$ 层 for 循环。当 $k$ 更大一些的时候,编写代码将变得十分繁琐。我们需要一个更加优秀的算法。
传统枚举中,需要固定 for 循环的层数,这样的后果就是程序非常丑陋冗长,而且不能随意增减枚举层数。
所以我们介绍一种新的基于递归的枚举算法,枚举每一个填空中所有可能的选项,然后判断这种选项是否合法。如果合法就继续填写下一个选项,然后继续;如果这个填空中的所有选项都不合法,那就不用继续枚举下去了,而是尝试更换上一个填空的选项,继续枚举。
这种方式被形象地称为回溯(Backtracking)算法,常使用深度优先搜索(Depth-First Search, DFS)来实现。这种如果已经不合法就不再继续往下递归的过程也被形象地称为剪枝(Pruning)。
我们先给出 DFS 的一般形式。
void dfs(int k) { // k 代表递归层数,或者说要填第几个空
if (所有空已经填完了) {
判断最优解 / 记录答案;
return;
} for (枚举这个空能填的选项) {
if (这个选项不合法) continue;
记录下这个空(保存现场);
dfs(k + 1);
取消这个空(恢复现场);
}
}基于这样的算法,我们给出本题的代码:
#include <iostream>
using namespace std;
const int N = 10;
int n, k, a[N];
void dfs(int pos) { // 需要填第 pos 位
if (pos > n) { // 当 n 位都已经填完时终止递归
for (int i = 1; i <= n; ++i) cout << a[i] << ' '; // 填完就输出
cout << '\n';
return;
} for (int i = 1; i <= k; ++i) {
a[pos] = i; // 将第 pos 位填入 i
dfs(pos + 1); // 继续填第 pos + 1 位
}
}
int main() {
cin >> n >> k;
solve(1); // 从第 1 位开始填
return 0;
}因为本题没有限制条件(每个空都可以填从 $1$ 到 $n$ 的任何数),每个空填的数都与之前填过的数无关,所以我们不需要记录填了什么,自然也就不需要回溯了。
当 $n = 2, k = 3$ 时,我们来看看上面这份代码的具体运行过程。
- 进入第 $1$ 层
dfs函数,$pos = 1$。要枚举第 $1$ 个位置的数字,先从 $1$ 开始,填入 $1$。继续递归dfs(2)。 - 进入第 $2$ 层
dfs函数,$pos = 2$。要枚举第 $2$ 个位置的数字,先从 $1$ 开始,填入 $1$。继续递归dfs(3)。 - 进入第 $3$ 层
dfs函数,$pos = 3$。要枚举第 $3$ 个位置的数字。先从 $1$ 开始,填入 $1$。继续递归dfs(4)。 - 进入第 $4$ 层
dfs函数,发现 $pos = 4$,意味着所有位置已经填写完毕,得到了一个合法的解,因此输出,然后返回上一层,也就是在dfs(3)中继续枚举 $2$、$3$,枚举完毕后就再返回上一层dfs(2),继续往后枚举。
为什么返回上一层还能继续枚举呢?这是因为计算机运行函数时,为每一个子函数都分配了一片栈空间(Stack Space),专门用于存储每一层递归函数的信息,当然就包括每层函数的各个局部变量的值了。
这样一来,即使 $n$ 和 $k$ 是变化的,我们也可以只用简单的一个函数搞定了。
有 $n$ 个元素,要求按字典序输出所有长度为 $k$ 的排列。$1 \le k \le n \le 10$。排列是从 $n$ 个不同元素中选取 $k$ 个元素($k \le n$),并按特定顺序进行安排的有序序列。
本题要求我们枚举排列,这就意味着不能有重复的元素。也就是说,当前这个空可以填什么,取决于我们之前填过了什么。
我们可以开一个 bool 数组 $vis$,用来记录之前哪些元素已经填过了,哪些没填过。枚举这个位置可以填的数时,如果发现这个数之前已经填过了,那么就直接 continue,也就是不填这个数。在填入这个数之后,我们需要也把它标记为“已经填过”,然后继续填下一个位置(进入下一层递归)。
下一层递归和之后的递归全部结束之后,要重新标记回“未填过”的状态,这样就不会影响接下来的填写了。
#include <iostream>
using namespace std;
const int N = 15;
int n, k, a[N];
bool vis[N];
void dfs(int pos) { // 需要填第 pos 位
if (pos > k) { // 当 n 位都已经填完时终止递归
for (int i = 1; i <= k; ++i) cout << a[i] << ' '; // 填完就输出
cout << '\n';
return;
} for (int i = 1; i <= n; ++i) {
if (vis[i]) continue;
a[pos] = i; // 将第 pos 位填入 i
vis[i] = true; // 将 i 标记为已填过
dfs(pos + 1); // 继续填第 pos + 1 位
vis[i] = false; // 取消标记(即标记为未填过)
}
}
int main() {
cin >> n >> k;
dfs(1); // 从第 1 位开始填
return 0;
}当 $n = 3, k = 2$ 时,来看看这份代码的具体运行过程。
- 进入第 $1$ 层
dfs函数,$pos = 1$。要枚举第 $1$ 个位置的数字,先从 $1$ 开始,填入 $1$。继续递归dfs(2)。 - 进入第 $2$ 层
dfs函数,$pos = 2$。要枚举第 $2$ 个位置的数字,先从 $1$ 开始。发现 $1$ 已经被填过了,跳过,然后填入 $2$。继续递归dfs(3)。 - 进入第 $3$ 层
dfs函数,发现 $pos = 3$,意味着所有位置已经填写完毕,得到了一个合法的解,因此输出,然后返回上一层,也就是在dfs(2)中继续枚举 $3$,枚举完毕后就再返回上一层dfs(1),继续往后枚举。
似乎和上一道题的枚举过程查不多,只是多了一个判断是否重复的过程。事实也确实如此,搜索的枚举过程大同小异,只是“枚举哪些东西”“判断合法性”和“枚举完毕之后做的事”上略有区别。
接下来我们来讨论一些更为复杂的情况。
讨论一种简化过的数独游戏——四阶数独。给出一个 $4 \times 4$ 的格子,每个格子都只能填写 $1$ 到 $4$ 的整数,要求每行、每列和四等分更小的正方形部分都刚好由 $1$ 到 $4$ 组成。下图给出了一个合法的四阶数独的例子。
给出空白的方格,问一共有多少种合法的填写方案。输出每一种方案,并在程序最后输出总的方案数。
回想枚举算法,最朴素的枚举方式是使用 $16$ 层 for 循环,一共要枚举 $4^{16} \approx 4 \times 10^9$ 种情况。现代计算机每秒约可处理 $10^7$ 次运算,显然远低于我们需要枚举的情况数量,不可行。
我们之前还讨论过枚举序列。既然每一行都是 $1$ 到 $4$,假设各行都是独立的,分别枚举 $4$ 个 $1$ 到 $4$ 的全排列,组成一个 $4 \times 4$ 的矩阵,然后判断这个矩阵是否符合数独的要求。我们使用类似计数排序的思路判断是否符合要求,也就是记录第 $i$ 行是否有 $1$、$2$、$3$、$4$,如果每个数字刚好都有一个,则说明这一行符合要求;列和小块同理。最多可能有 $(4 \times 3 \times 2 \times 1)^4 \approx 3 \times 10^5$ 种情况,完全可以在一秒钟内运行出结果。
然而,这样的解法仍然有很多浪费:如果第一行是 $\{1, 2, 3, 4\}$,第二行第一列是 $1$,后面不管怎么填写,都不符合要求,但还是要继续进行无谓的枚举然后判断。我们希望可以有一个算法,在枚举序列的时候,一旦发现某位数字不符合要求,就立刻中断这种情况的枚举,直接枚举下一情况。这样可以在很大程度上节约程序的运行时间。
现在你学过搜索了,问题就变得简单很多了。我们给出这道题的代码:
#include <iostream>
using namespace std;
const int N = 5;
int a[N * N], n = 4 * 4, ans; // 全局变量不赋值默认初始化为 0
bool b1[N][N], b2[N][N], b3[N][N]; // 分别记录横行,竖行,四个小块
void dfs(int x) { // 第 x 个空填什么
if (x > n) { // 如果所有空已经填满
++ans; // 增加结果数量
for (int i = 1; i <= n; ++i) { // 输出放置方案
cout << a[i] << ' ';
if (i % 4 == 0) cout << '\n'; // 每输出四个元素就换行一次
} return;
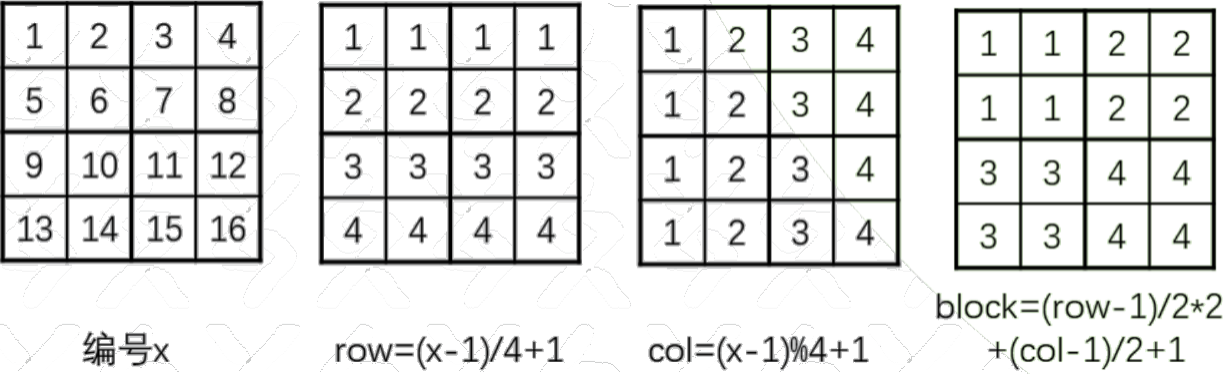
} int row = (x - 1) / 4 + 1; // 横行编号
int col = (x - 1) % 4 + 1; // 竖行编号
int block = (row - 1) / 2 * 2 + (col - 1) / 2 + 1; // 小块编号
for (int i = 1; i <= 4; ++i) {
if (b1[row][i] || b2[col][i] || b3[col][i]) continue; // 如果已经出现过就跳过
a[x] = i; // 记录放置位置
b1[row][i] = true, b2[col][i] = true, b3[block][i] = true; // 标记为已经出现过
dfs(x + 1); // 下一层递归
b1[row][i] = false, b2[col][i] = false, b3[block][i] = false; // 取消标记
}
}
int main() {
dfs(1); // 从第 1 个空开始枚举
cout << ans << '\n';
return 0;
}如何保证放置的位置合法呢?我们使用数组 $b1$、$b2$、$b3$ 来记录横行、竖行、四个小块中的每个数字 $i$ 是否被占用。如果都没有被占用,说明可以填入。把这些空格编号为 $1$ 到 $16$,每个格子所占的行号、列号和小块编号就都可以计算出来了。
对于这份代码,它的搜索和回溯的详细步骤如下:
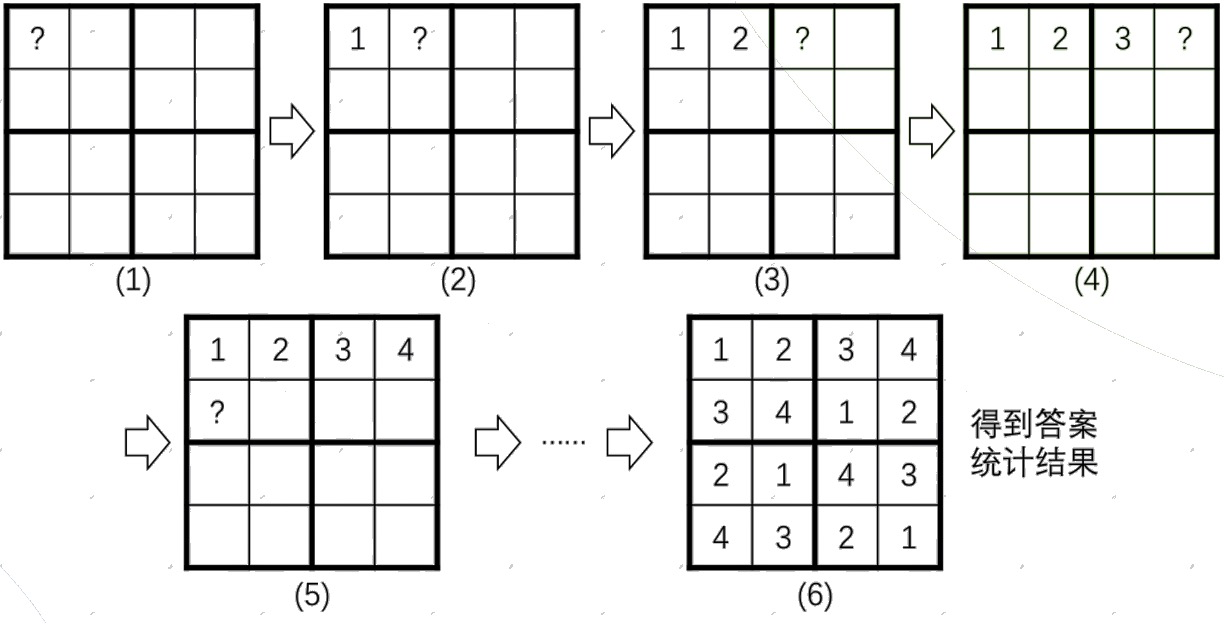
- 进入第 $1$ 层
dfs函数,$x = 1$。要枚举第 $1$ 个格子的数字,先从 $1$ 开始。这里填 $1$ 没有问题,就把 $1$ 记录下来,同时需要记录第 $1$ 行、第 $1$ 列、第 $1$ 小块中“$1$”已经被填写过了,继续递归dfs(2)。 - 进入第 $2$ 层
dfs函数,$x = 2$。要枚举第 $2$ 个格子的数字,先从 $1$ 开始,发现第一行已经有 $1$ 了,不行;于是尝试填入 $2$,没问题,就记录 $2$,同时记录第 $1$ 行、第 $2$ 列、第 $1$ 小块中“$2$”已经填写过了,继续递归dfs(3)。 - 进入第 $3$ 层
dfs函数,$x = 3$。要枚举第 $3$ 个格子的数字。填写 $1$ 和 $2$ 是不行的,但是可以填写 $3$。同时记录下第 $1$ 行、第 $3$ 列、第 $2$ 小块中“$3$”已经填写过了,继续递归dfs(4)。 - 进入第 $4$ 层
dfs函数,$x = 4$。要枚举第 $4$ 个格子的数字。这里只能填写 $4$ 了,然后记录下来,继续递归dfs(5)。 - 进入第 $5$ 层
dfs函数,$x = 5$。要枚举第 $5$ 个格子的数字。$1$ 不行(第一列重复),$2$ 也不行(第一小块重复),填写 $3$,同时记录第 $2$ 行、第 $1$ 列、第 $1$ 小块“$3$”已经填写过了,继续递归dfs(6)。 - ……
- 一直到
dfs(16)填写完最后一个数字 $1$ 后,继续递归dfs(17)。发现 $x = 17$ 意味着所有格子已经填写完毕,得到了一个合法的解,因此记录答案,然后返回上一层,也就是在dfs(16)中继续枚举 $2$、$3$、$4$……如果没有可行解,就再返回上一层dfs(15),继续往后枚举。
如果在运行到某一层的时候所有选项都不是合法的,那么自然是不能往下面递归的。遇到这种情况,就返回上一层,然后继续枚举。
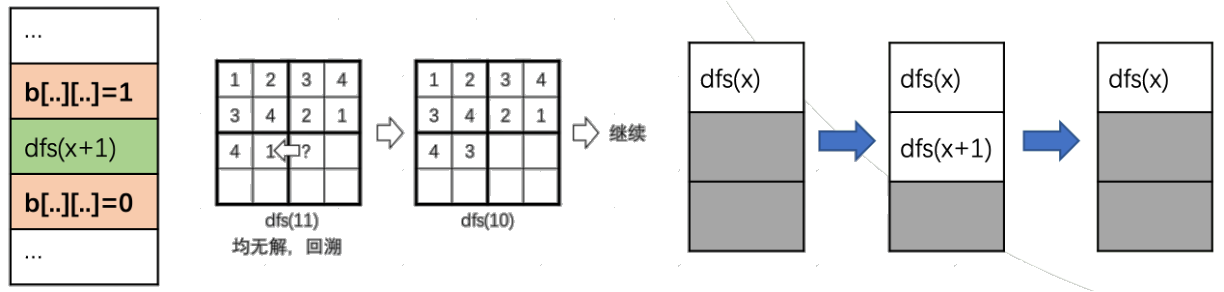
如上图,在 dfs(11) 中所有选项均不合法,就回退到 dfs(10)。原来的 dfs(10) 中 $i = 1$,于是就继续枚举剩余的选项,比如 $i = 2$(不合法),$i = 3$(合法),然后继续前进到 dfs(11)。
在 $n \times n$ 的国际象棋棋盘上放置 $n$ 个皇后使得她们互不攻击。皇后的攻击范围时同一行、同一列、在同斜线上的其他棋子。$n \le 13$,求方案数,并输出前 $3$ 种放法。
这题是 DFS 的超级经典的例题。
我们考虑到每一行只能放一个,且所有行放在第几列都是不相同的,所以可以对 $n$ 进行枚举全排列(这样就能保证皇后不会攻击到同一行、同一列的其他皇后),然后判断是否有两个皇后在统一斜线上。这种方法比较低效,可以考虑使用搜索回溯算法进行优化。
假设 $n = 4$,那么求解可以认为是将 $1$、$2$、$3$、$4$ 填入 $4$ 个空中,代表每一行第几列有一个棋子。填空的时候保证填入的棋子不会和之前的棋子冲突。
因为分行枚举棋子位数,所以每行不会冲突。在这里使用 $b1$ 数组,记录下 $b1_i$ 说明第 $i$ 列已经被占。
那如何记录某一个斜排已经被占呢?可以发现,对于同一个斜行上的所有坐标点 $(x, y)$ 中,$x + y$ 或 $x - y$ 是定值,因此设立 $b2$ 和 $b3$ 数组,$b2_i$ 用来记录 $x + y = i$ 的斜线是否被占用,$b3_i$ 用来记录 $x - y + 15 = i$ 的斜线是否被占用。注意,因为 $x - y$ 可能小于 $0$,普通的数组的下标不能为负数,因此我们加上 $15$ 的偏移量,来保证下标非负。
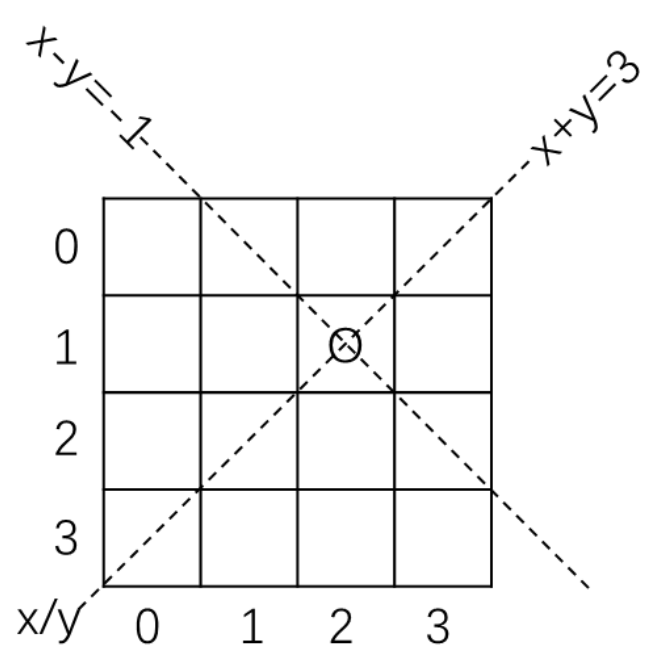
通过这三个数组,就可以判断出打算填写的位置是否被占(竖排、斜排)。如果被占了,就不能填写在这个位置了。
例如,$n = 4$ 时,搜索过程如下:
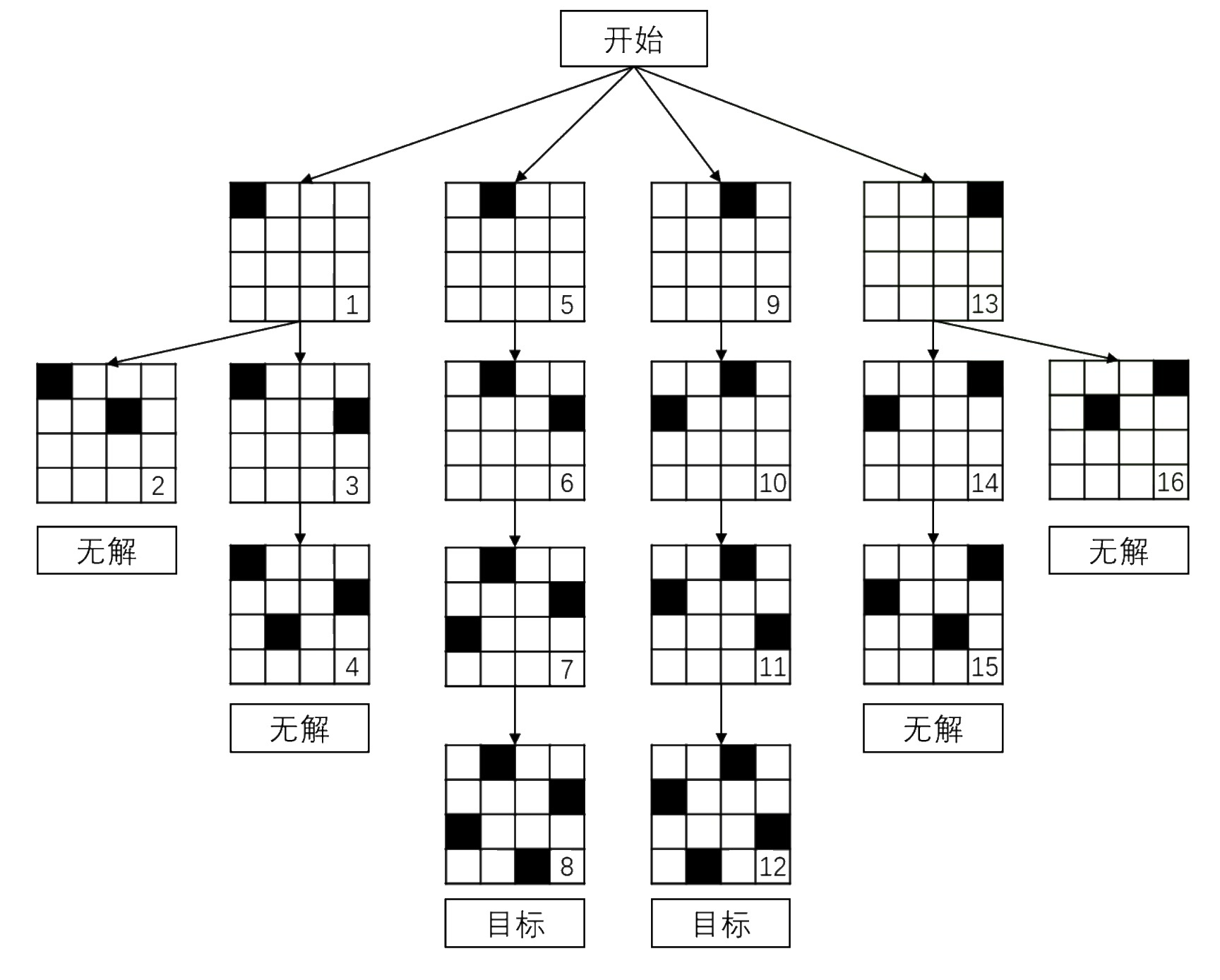
由此,我们就可以写出本题的代码了。
#include <iostream>
using namespace std;
const int N = 100;
int n, a[N], ans;
bool b1[N], b2[N], b3[N]; // 分别记录 y、x + y、x - y + 15 是否被占用
void dfs(int x) { // 第 x 行的皇后放哪儿
if (x > n) { // 如果所有皇后已经放置
++ans; // 增加结果数量
if (ans <= 3) { // 输出前 3 种答案
for (int i = 1; i <= n; ++i) cout << a[i] << ' ';
cout << '\n';
} return;
} for (int i = 1; i <= n; ++i) {
if (b1[i] || b2[x + i] || b3[x - i + 15]) continue;
a[x] = i; // 记录放置位置
b1[i] = true, b2[x + i] = true, b3[x - i + 15] = true; // 标记占位
dfs(x + 1); // 下一层递归
b1[i] = true, b2[x + i] = true, b3[x - i + 15] = true; // 取消标记
}
}
int main() {
cin >> n;
dfs(1); // 从第 1 行开始枚举
cout << ans << '\n';
return 0;
}由此,我们总结出了两种常见的需要用到 DFS 的场景。
- 遇到了需要枚举序列的时候,搜索回溯会很好⽤。不需要⽣成所有的序列全排列,⽽是⼀个⼀个地填空,保证填空的时候序列是合法的,这样就可以不⽤枚举很多⽆效序列,节约程序运⾏时间。
- 对于一些枚举或者枚举子集的问题,可以使用搜索回溯来解决。但如果需要枚举的元素比较多(超过几十个),即使是搜索回溯也相当慢。我们将在之后会学到的动态规划中讨论这一情况。
DFS 在笔者初学时就遇到了相当大的困难,但这又是比赛中十分重要的拿分技巧,因此请务必认真完成此处的练习。
