更佳的阅读体验：2023 国庆集训 Day 6B 笔记，本文同步发表于 洛谷博客。

以下内容为个人总结，如有错误或您有不同见解，欢迎指出。

矩阵

矩阵的运算

加 / 减法

• 两个 一样大 的矩阵，对应位置相加 / 减。

乘法

• 要求 $n \times m$ 的矩阵与 $m \times k$ 的矩阵相乘，即第一个矩阵的列数等于第二个矩阵的行数。
• 结果是一个 $n \times k$ 的矩阵，即行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。

$$ \left[\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\right] \times \left[\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}\right] = \left[\begin{matrix} 9 & 12 & 15 \\ 19 & 26 & 33 \end{matrix}\right] $$

struct matrix {
    int n, m;  // 矩阵的行数 列数
    int a[20][20];  // a[i][j] 代表矩阵第 i 行第 j 列
    matrix() {  // 构造函数
        n = m = 0;
        memset(a, 0, sizeof(a));
    }
};

matrix operator*(const matrix &m1, const matrix &m2) {  // 计算 m1 * m2, O(n^3)
    matrix m3;  // 结果矩阵
    m3.n = m1.n, m3.m = m2.m;
    for (int i = 1; i <= m3.n; ++i)
        for (int j = 1; j <= m3.m; ++j)  // 计算结果矩阵中第 i 行第 j 列的数
            for (int k = 1; k <= m1.m; ++k)
                m3.a[i][j] += m1.a[i][k] * m2.a[k][j];
    return m3;
}

矩阵快速幂

求矩阵 $x$ 的 $y$ 次方。

• 单位矩阵：主对角线为 $1$ 其余为 $0$ 的矩阵 $I = \left[\begin{matrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{matrix}\right]$。

matrix qpow(const matrix x, int y) {  // 计算 x 的 y 次方
    matrix ans;
    ans.n = ans.m = x.n;
    for (int i = 1; i <= x.n; ++i) ans.a[i][i] = 1;
    while (y) {
        if (y & 1) ans = ans * x;
        x = x * x, y >>= 1;
    } return ans;
}

洛谷 P1962 - 斐波那契数列

• 构造一个矩阵 $\left[\begin{matrix} f_i & f_{i - 1} \end{matrix}\right]$​ 和 $\left[\begin{matrix}1 & 1 \\ 1 & 0\end{matrix}\right]$，可得：

$$ \left[\begin{matrix} f_1 & f_0 \end{matrix}\right] \times \left[\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix}\right] ^n = \left[\begin{matrix} f_{n + 1} & f_n \end{matrix}\right] $$

• 使用矩阵快速幂求解，时间复杂度 $O(\log n)$。

递推矩阵

• 决定矩阵大小的因素：和前几项有关，例如洛谷 P1939 【模板】矩阵加速（数列）。

$$ \left[\begin{matrix} a_i & a_{i - 1} & a_{i - 2} \end{matrix}\right] \times \left[\begin{matrix} \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \end{matrix}\right] = \left[\begin{matrix} a_{i + 1} & a_i & a_{i - 1} \end{matrix}\right] $$

BZOJ #2396. 神奇的矩阵

• 对于 $N \le 10^3$，直接矩阵乘法显然会超时。
• 对于矩阵 $A$，$B$，$C$，直接进行 $A \times B = C$ 会达到 $O(n^3)$。
• 考虑构造一个 $1 \times n$ 的矩阵 $D$，计算 $D \times A \times B = D \times C$，每次乘法都是 $1 \times n$ 的矩阵，时间复杂度 $O(n^2)$。
• 随机一个 $D$，与 $A \times B$ 和 $C$ 相乘并进行比较，显然正确率非常高。

逆元

• 用于模意义下的除法。
• 费马小定理：当 $p$ 是质数，如果有 $a$ 满足 $\gcd(a, p) = 1$，则有 $a^{p - 1} \equiv 1 (\mod p)$。
• 对上述同余式两边同时除以 $a$，得到 $a^{p - 2} \equiv a^{-1} (\mod p)$，即模 $p$ 意义下 $a^{p - 2}$ 与 $a^{-1}$ 相同。
• 所以，$a$ 在模 $p$ 意义下的逆元为 $a^{p - 2}$。

组合数学

• $C(n, m)$ 表示从 $n$ 个数中选择 $m$ 个 不同顺序算一种方案 的总方案数。

$$ C(n, m) = \frac{n(n - 1)(n - 2) \cdots (n - m + 1)}{m!} = \frac{n!}{m!(n - m)!} $$

性质

• 组合数的递推式：$C(n, m) = C(n - 1, m - 1) + C(n - 1, m)$。
• 从以上递推式可以得到杨辉三角，则左对齐的杨辉三角上第 $i$ 行第 $j$ 列的数即为 $C(i, j)$。

Example

给定三个数 $n$，$m$，$p$，求 $C(n, m) \mod p$。

Subtask 1: $n, m \le 1000$

• 递推预处理杨辉三角。

int c[N][N];
for (int i = 0; i <= n; ++i) {
    c[i][0] = 1;
    for (int j = 1; j <= i; ++j)
        c[i][j] = c[i - 1][j - 1] + c[i - 1][j] % p;
}

• 练习题：洛谷 P2822 [NOIP2016 提高组] 组合数问题。

Subtask 2: $n, m \le 10^6$，$p \approx 10^9$，且 $p$ 是质数

• 预处理阶乘以及阶乘的逆元。

int fac[N], ifac[N];  // fac[i] 代表 i! % p, ifac[i] 代表 1 / i! % p

fac[0] = 1;
for (int i = 1; i < N; ++i)
    fac[i] = 1ll * fac[i - 1] * i % p;
for (int i = 0; i < N; ++i)
    ifac[i] = qpow(fac[i], p - 2);

int C(int n, int m) {  // 求 C(n, m) % p, C(n, m) = n! / m! / (n - m)!
    return 1ll * fac[n] * ifac[m] % p * ifac[n - m] % p;
}

Subtask 3: $n \le 10^9, m \le 10^3, p \le 10^9$，$p$ 不保证是质数

• 使用公式 $C(n, m) = \frac{n(n - 1)(n - 2) \cdots (n - m + 1)}{m!}$。
• 因为结果一定是整数，则分子一定是分母的倍数。
• 求 GCD。

int fenzi[N], fenmu[N];  // 分子，分母

int C(int n, int m) {
    for (int i = 1; i <= m; ++i) {
        fenzi[i] = n - i + 1;
        fenmu[i] = i;
    } for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= m; ++j) {
            int g = __gcd(fenzi[i], fenmu[j]);
            fenzi[i] /= g, fenmu[j] /= g;
        }
    int ans = 1;
    for (int i = 1; i <= m; ++i)
        ans = 1ll * ans * fenzi[i] % p;
    return ans;
}

概率和期望

加法原理与乘法原理

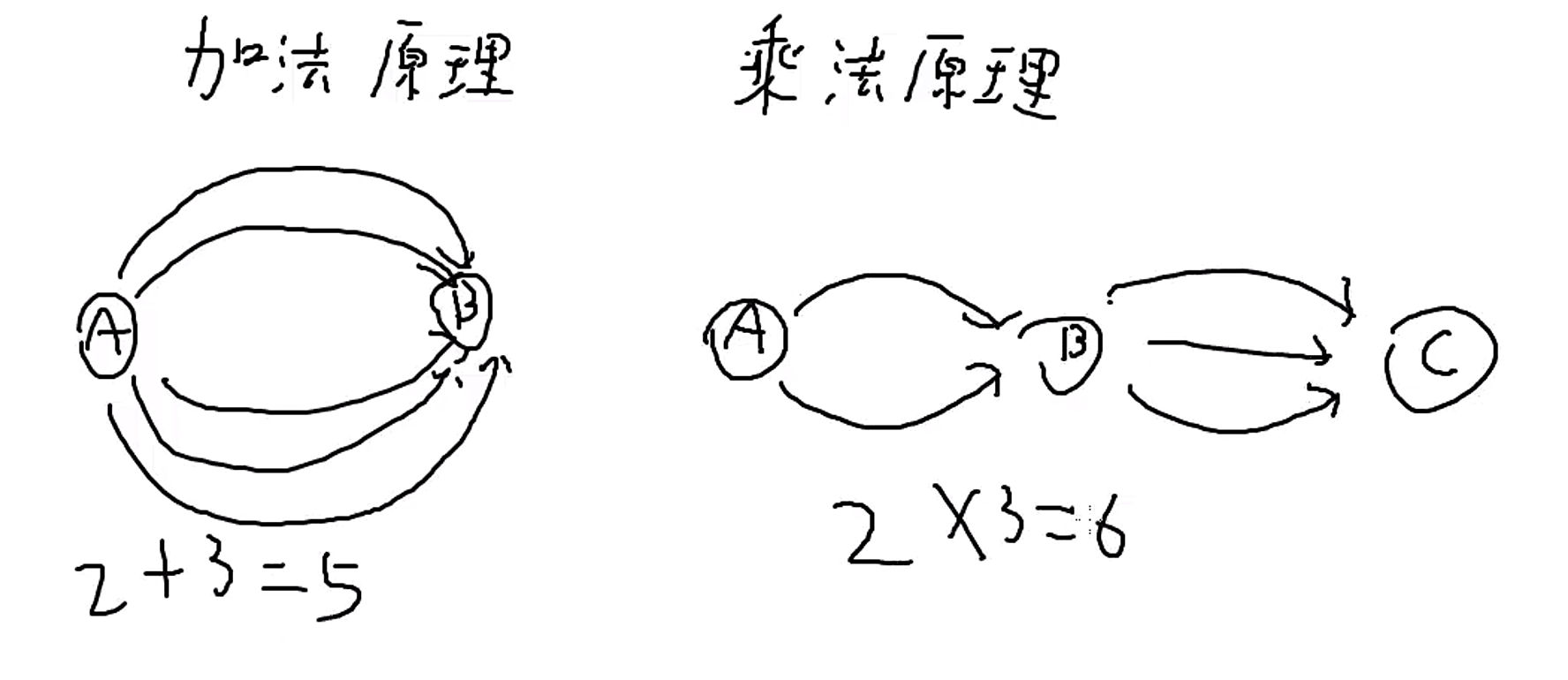
• 加法原理：同阶段互斥；
  乘法阶段：不用阶段不互斥。

条件概率

• 已知事件 $B$ 发生时事件 $A$ 发生的概率 $P(A|B)$。

Example 1

假设有 $3$ 张形状相同的卡片，其中一张两面都是黑色，一张两面都是红色，另一张是一面红一面黑，随机取出一张放在桌上，朝上的面为红色，那么另一面是黑色的概率是多少？

• 得到答案 $\frac{1}{3}$。

Example 2

$n$ 个人按任意顺序一次抓阄，每个人抓完阄后立即打开，当某个人抓到「中」时，整个抓阄过程结束（后面的人就不必抓了）。问：此种抓阄方式是否公平，请说明理由。

• 每个人的概率都是 $\frac{1}{n}$，公平。

Example 3

在小葱和小泽面前有三瓶药，其中有两瓶是毒药，每个人必须喝一瓶。小葱和小泽各自选了一瓶药，小泽手速比较快，将药喝了下去，然后就挂掉了。小葱想活下去，它是应该喝掉手上的这瓶，还是另外剩下的一瓶呢？

• 无论是否更换手上的药水，小葱挂掉的概率为 $50 \%$，则换与不换答案不变。

Example 4

小葱想要过河，有两条路：

• 一条路有 $100$ 个石头，每个石头有 $\frac{1}{100}$ 的概率会挂掉。
• 另一条路有 $1000$ 个石头，每个石头有 $\frac{1}{1000}$ 的概率会挂掉。

小葱应该走哪边呢？（请勿使用计算器）

• 走第一条路活下来的概率为 $(\frac{99}{100})^{100}$，走第二条路活下来的概率为 $(\frac{999}{1000})^{1000}$。
• 整理并约分后得到 $(\frac{99}{100})^{100} < (\frac{999}{1000})^{1000}$，所以应该走第二条路。

Example 5

小泽在数轴上的点 $0$ 处。

小泽每次有 $r$ 的概率向右走，有 $1 - r$ 的概率向左走，问小泽走到 $-1$ 的概率。

• 令答案为 $p$，得到 $p = (1 - r) + rp^2$，解得 $p = \frac{1 - r}{r}$。
• 思考当 $r < \frac{1}{2}$ 时 $p$ 的值。此时应有 $p = 1$。

期望

• $\sum$ 每一种情况的权值 $\times$ 这种情况的概率。
• 和的期望等于期望的和：$E(X_1 + X_2) = E(X_1) + E(X_2)$。

BZOJ #2969. 矩形粉刷

• 令第 $i$ 行第 $j$ 列的格子为 $x_{i, j}$，$x_{i, j} = 0$ 时表示这个格子没有被刷，$x_{i, j} = 1$ 表示这个格子已经被刷。
• 令 $X=被刷格子数量$，得到 $E(X) = E(x_{1,1} + x_{1, 2} + \cdots + E_{n, m})$。
• 令 $p_{i, j}$ 为第 $i$ 行第 $j$ 列的格子被刷过的概率，则 $E(X) = \sum p_{i, j}$。
• 总情况数为 $n^2m^2$，能刷掉 $(i, j)$ 的方案数为 $i(n - i + 1) \cdot j(m - j + 1)$，则只刷一次刷掉 $(i, j)$ 的概率 $q_{i, j} = \frac{i(n - i + 1) \cdot j(m - j + 1)}{n^2m^2}$，一次刷不掉的概率为 $1 - q_{i, j}$，$k$ 次刷不掉的概率为 $(1 - q_{i, j})$。
• 得到 $p_{i, j} = 1 - (1 - q_{i, j})^k$，所以 $E(X) = \sum p_{i, j} = \sum [1 - (\frac{i(n - i + 1) \cdot j(m - j + 1)}{n^2m^2})^k]$。