本文将会不定期的补充各种关于高中数学的知识。

感谢我的朋友 RyanLi 先生为我提供放置博客的地方。

关于直线与点 - 2025.8.22

众所周知，直线的方程可以写作 $l:Ax+By+C=0$。然而，我们会惊异的发现，对于不在直线上的一个点 $P(x_0,y_0)$ 来说，量 $|Ax_0+By_0+C|$ 经常出现在我们的方程中。那么它代表什么意思呢？

我们可以大概猜出，$A,B$ 和直线的斜率有关，那么我们当然可以选取两个直线上的点 $A(x_A,y_A),B(x_B,y_B)$，那么

$$Ax_A+By_A+C=0$$
$$Ax_B+By_B+C=0$$

两式相减得到

$$A(x_A-y_A)+B(y_A-y_B)=0$$

用向量的表示法，我们得到

$$(A,B)\cdot\overrightarrow{AB}=0$$

由于 $\overrightarrow{AB}$ 表明了直线的方向，而 $(A,B)$ 与 $\overrightarrow{AB}$ 垂直，故而我们可以姑且认为，$\overrightarrow n_l=(A,B)$ 代表了曲线的法向量。所以，对于 $Ax_0+By_0+C$，我们可以将它减去 $0$，然后令 $Q(p,q)$ 为直线上的任一点，就有

$$|A(x_0-p)+B(y_0-q)|=|\overrightarrow n\cdot\overrightarrow{PQ}|$$

我们可以满意的得到，上面的量代表了法向量与该点到直线上任意一点的点积，这样我们就设法求出了该点到直线的距离。现在除以法向量的长度 $|(A,B)|$，我们就拿到了点到直线的距离公式

$$\delta(P,l)=\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}$$

这里 $\delta(P,l)$ 代表有向距离，正负号代表 $P$ 在 $l$ 的“哪一侧”。

好的，现在我们当然可以试着推导点关于直线的对称点公式。我们给定点 $P(x_0,y_0)$ 并保证其不在直线 $Ax+By+C=0$ 上，那么我们当然可以用用刚刚的结论，即用法向量乘以两倍的坐标距离，不过是有向距离。

所以 $P$ 的对称点 $P'$ 的坐标为 $\left(x_0-\dfrac{2A\delta(P,l)}{\sqrt{A^2+B^2}},y_0-\dfrac{2B\delta(P,l)}{\sqrt{A^2+B^2}}\right)$，用向量写则是 $\overrightarrow{PP'}=2\delta(P,l)\hat n$，其中 $\hat n$ 代表法向量的单位向量，即 $\hat n=\overrightarrow n/|\overrightarrow n|$。

对于直线关于直线对称，我们理解成点就完了，可惜并没有这样简单。如果 $l:Ax+By+C=0$ 和 $l'$ 关于 $m:Dx+Ey+F=0$ 对称，那么 $l'$ 的方程就是
$$\frac{Ax+By+C}{Dx+Ey+F}=\frac{2(AD+BE)}{D^2+E^2}$$
按照刚才的分析，等式等价于
$$\frac{|\overrightarrow{n_l}|d(P,l)}{|\overrightarrow{n_m}|d(P,m)}=\frac{2\overrightarrow{n_{l}}\cdot\overrightarrow{n_{m}}}{\overrightarrow{n_m}^2}$$
显然，它等价于
$$\frac{\delta(P,l)}{2\delta(P,m)}=\cos\langle l,m\rangle$$

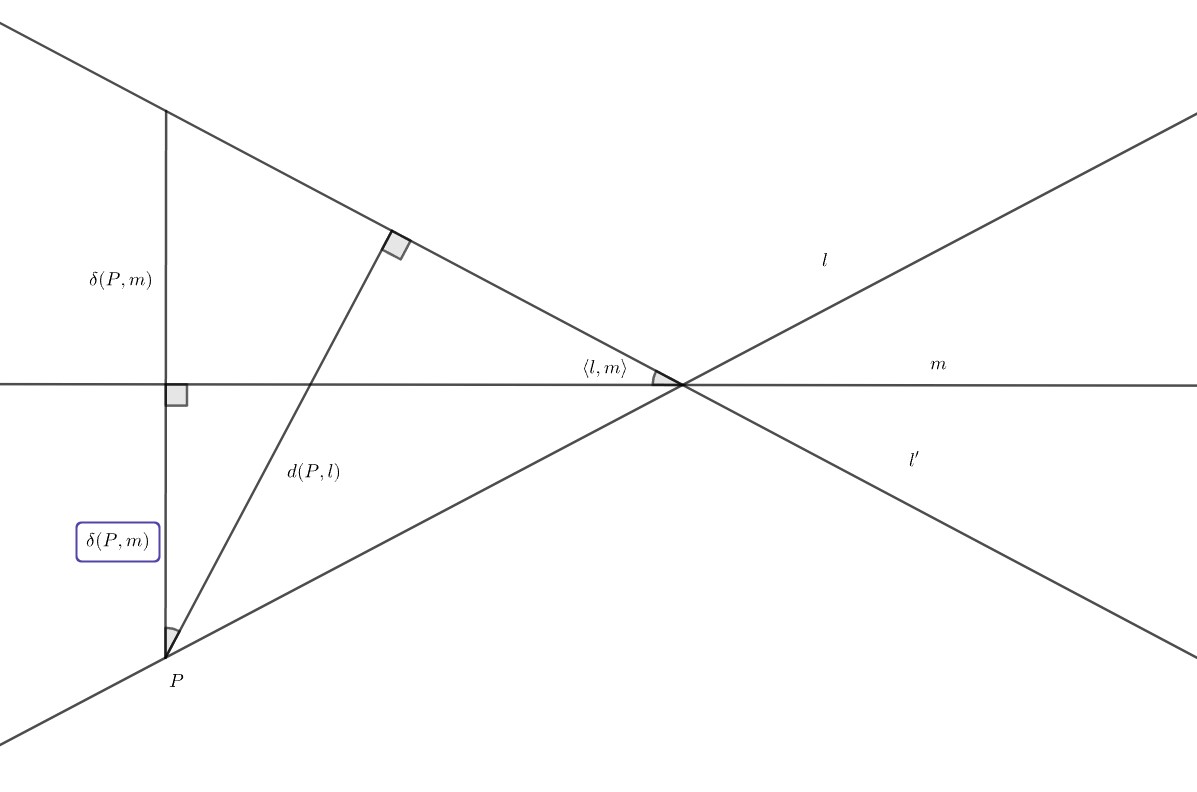
看图即可理解。

关于圆锥曲线

所有的圆锥曲线都满足第零定义，即在二对立全等圆锥上用平面截出的曲线。很不幸，因为它过于几何，所以没人用它。

我们首先给出所有圆锥曲线都满足的第二定义：

圆锥曲线 $\Gamma$ 满足平面内动点 $P$ 到某定点 $F$ 的直线的距离和到某定直线 $l$（满足 $F\not\in l$）的距离之比为正常数 $e$。其中 $e$ 称为离心率，$F$ 称为焦点，$l$ 称为准线。当 $0<e<1$ 时，$\Gamma$ 为椭圆；当 $e=1$ 时，$\Gamma$ 为抛物线；当 $e>1$ 时，$e$ 为双曲线。

好的，也许它有点用，但是现在我们用不着他。下面我们给出三种最常见的椭圆曲线方程，及其几何意义的理解。

对于椭圆，我们知道
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
想要理解它，我们可以取 $(\pm a,0),(0,\pm b)$ 四点（原因是这四个点是最容易满足方程的），在它上面做一个平行于坐标轴的矩形，它恰好能框柱整个矩形。此时，我们取任意一个焦点 $F(c,0)$，让它和 $(0,b)$ 连上，我们就发现斜边长等于 $a$。这是显然的，因为这个方程可以被改为这样：
$$\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1$$

对于双曲线，方程就是对 $1/b^2$ 项变号：
$$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$
但是事实上，我们发现它其实可以表达成
$$\frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1$$
所以我们发现，$b^2=|a^2-c^2|$。对于理解这个方程，我们首先把 $1$ 改成 $0$，此时我们发现方程变成了 $x^2/a^2=y^2/b^2$，也即 $x/y=\pm a/b$，我们拿到了渐近线；而后，我们让 $x=\pm a$，这样我们便拿到了它的顶点，于是乎我们用渐近线和两点再次框出一个平行于坐标轴的矩形，而它的对角线的一半就是 $c$。

对于抛物线，我们知道它的定义直接采用了第二定义，即到直线距离和焦点距离都为 $p$ 的点。而在（一般的）高中数学题中，抛物线的顶点都是原点，且没有旋转，这样我们可以找到焦点和准线，它们都在 $x=\pm p/2$ 上。