图论、构造、图兰定理

Solution 1：构造一个二分图 $G$，使得 $G$ 对于 $n \in \operatorname{odd}$ 满足左右两部点数量之差为 $1$，对于 $n \in \operatorname{even}$ 满足左右两部点数量相等，在 $n=4$ 时的图 $G$ 如下，加粗部分和未加粗部分即左部点和右部点。

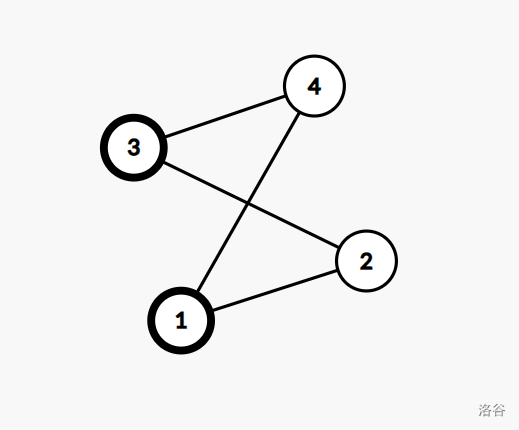
每次在点数较少的部点添加一个新点，然后从新点向另一部点中的所有点连边即可得到边数最大且无三元环的图。特判 $n \leq 3$ 时的答案，对于 $n \geq 4$ 的情况递推求解。

Solution 2：图兰定理：一个有 $n$ 个节点并且不存在三元环的图的边数不超过 $\left\lfloor \dfrac{n^2}{4} \right\rfloor$。